Convergence: From "The Limit of Equations" to "The Limit of Growth"

In economics courses, most concepts often undergo “mathematical meaning - economic meaning - statistical meaning” three re-understandings. We often see the same thing in different places, but we rarely take the time to fully understand it in one go, for example, three calculation formulas.

This article will summarize the concept of “convergence” as it runs through these three stages (although the connections may seem weak, I still want to go through it all at once).

I. Advanced Mathematics: Limits and Convergence

Limits and convergence are essentially the same thing from the start.

Main reference: Tongji Edition “Advanced Mathematics”¹, where convergence is introduced as a description of the state of a limit:

In the limit of a sequence (page 21, Volume I), the sequence $x_n$ converges to $a$, denoted as $\lim_{n \rightarrow \infty}{x_n=a}$.

In the limit of a function (page 33, Volume I), the function converges, denoted as $\small \lim_{n \rightarrow \infty}{f(x_n)}=\lim_{n \rightarrow x_0}{f(x)}$.

In the limit of a series (page 252, Volume II), $\small s=u_1+u_2+u_3+…u_i+…$ an infinite series converges if $\lim_{n \rightarrow \infty}{s_n=s}$, otherwise it diverges.

$$ \text{Convergence Classification} \begin{cases} \text{Content} \begin{cases} \text{Absolute Convergence} \ \text{Conditional Convergence} \end{cases} \ \text{Form} \begin{cases} \text{Pointwise Convergence} \ \text{Uniform Convergence} \end{cases} \end{cases} $$

Where series convergence is further divided into absolute convergence and conditional convergence; pointwise convergence and uniform convergence.

Absolute Convergence: If $\small \sum_{n=1}^{\infty}{|u_n|}$ converges, then $\small \sum_{n=1}^{\infty}{u_n}$ is absolutely convergent.

Conditional Convergence: If $\small \sum_{n=1}^{\infty}{|u_n|}$ does not converge, but $\sum_{n=1}^{\infty}{u_n}$ converges, then $\small \sum_{n=1}^{\infty}{u_n}$ is conditionally convergent.

Pointwise Convergence: $\small \exists{0<x<\delta},\forall\varepsilon>0, |f(x)-A|<\varepsilon$, $\small \exists{0<x<\delta},\forall\varepsilon>0, |f(x)-A|<\varepsilon$

Uniform Convergence: $\small \exists{0<|x_1-x_2|<\delta},\forall\varepsilon>0,|f(x_1)-f(x_2)|<\varepsilon$, $\small \exists{0<|x_1-x_2|<\delta},\forall\varepsilon>0,|f(x_1)-f(x_2)|<\varepsilon$

By the way, convergence radius, which is the range of $x$ values that allow the series $\small u_n(x)$ to converge.

Is there a shortcut for judging convergence or divergence? My advanced mathematics teacher mentioned a “humorous” method, which I also came across on Zhihu:

Look at these two characters, aren’t they both convergent and divergent?

II. Probability Theory: Law of Large Numbers and Central Limit Theorem

What you think of as “chance” is often embedded in “necessity.” Someone necessarily wins the lottery; it’s just that person chance is you.

Reference: Mao Shisong’s “Probability Theory and Mathematical Statistics”², sequences of random variables have two modes of convergence: convergence in probability and convergence in distribution.

Convergence in Probability: $\bbox[#def,5px,border: 1px solid]{ x\stackrel{P}{\longrightarrow}c }$

For example, when flipping a coin, the initial frequency of heads may deviate greatly from $\frac{1}{2}$, but as the number of flips increases, the frequency approaches the probability. Frequency statistics have become one of the methods to determine probability³.

Various versions of the Law of Large Numbers, $\boxed{ Law of Large Numbers }$ essentially say the same thing: as the number of experiments $n$ increases, the probability of the deviation $\small \frac{S_n}{n}-P$ being greater than a predetermined value $\varepsilon$ decreases.

Whether it’s the Bernoulli (Bernoulli) Law of Large Numbers, Chebyshev’s Law of Large Numbers, Markov’s Law of Large Numbers, or Khinchin’s Law of Large Numbers, they all essentially describe the same thing⁴.

Convergence in Distribution: $\bbox[#def,5px,border: 1px solid]{ x\stackrel{F}{\longrightarrow}c }$

Strong convergence in distribution is pointwise convergence, while weak convergence removes discontinuities and only considers the continuous distribution of $F(x)$.

Denoted as $ \mathbb{P}(X_n\leqslant a)\to\mathbb{P}(X\leqslant a) $, which is $ \lim_{n\to\infty}F_n (x)=F (x)$.

The $\boxed{ Central Limit Theorem }$ states that under certain conditions⁵, the distribution function of the sum of independent random variables $Y_n=\sum_{i=1}^{n}{X_i}$ approaches a normal distribution.

Interesting knowledge about function distributions⁶

• Assume there is a random variable that follows a binomial distribution.
• When it tends to the limit, with the expectation equal to the variance, it becomes a Poisson distribution.
• The intervals between random variables follow an exponential distribution.
• The nth variable corresponds to the gamma distribution in the horizontal coordinate.

III. Economic Significance: Convergence Effect

Money ≠ Numbers, Operations ≠ Problems, Economics ≠ Mathematics

1. Convergence Hypothesis (Convergence)

From the资料 used by the teacher in the “Regional Economics” course 《Advanced Economic Geography》 (He Canfei著).

With the proposal of the Solow model, development economics researchers raised questions:

Since each economy has its own steady state and balanced growth path,

and at the same time, less developed economies grow quickly while advanced economies slow down,

the question is, will the economic growth of all economies converge in the end?

$$ \begin{cases} \beta\text{-convergence} \begin{cases} \text{Absolute Convergence} \ \text{Conditional Convergence} \ \text{Club Convergence} \end{cases} \ \sigma\text{-convergence} \end{cases} $$

$\beta$-convergence:

• $\boxed{\beta\text{ Absolute Convergence}}$ assumes that regardless of the initial conditions of the economy, due to the faster development of the weaker and slower development of the stronger, the economy will eventually converge to the same level. All we need is a little patience.
• $\boxed{\beta\text{ Conditional Convergence}}$ assumes that the growth rate of the economy is influenced by certain structural factors (such as population structure, endowments of factors, growth rates of factors), so different economies converge to different steady states, and the final outcomes of development differ.
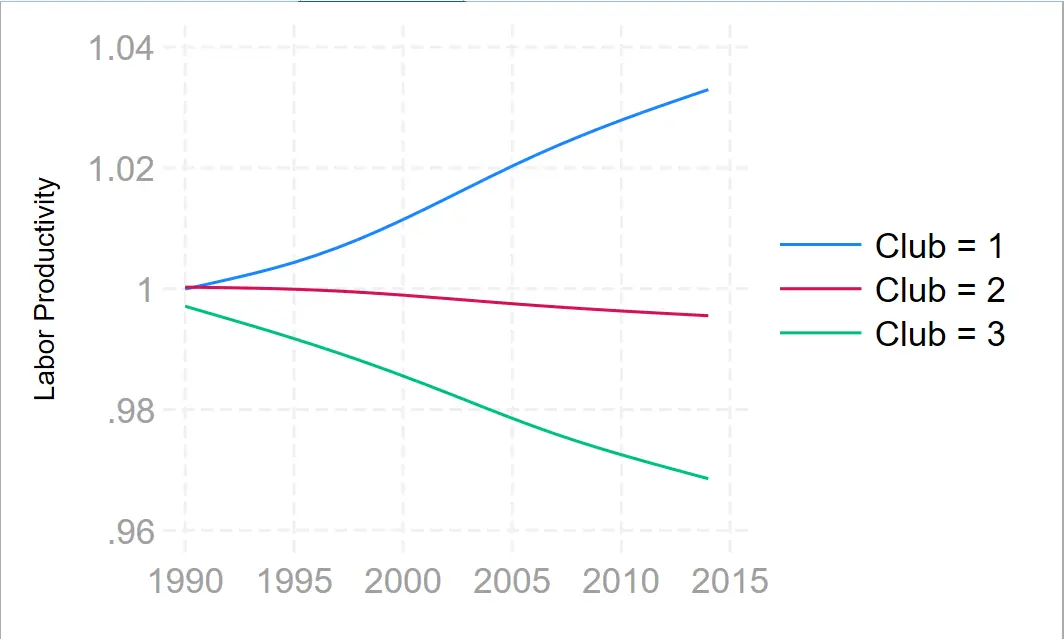
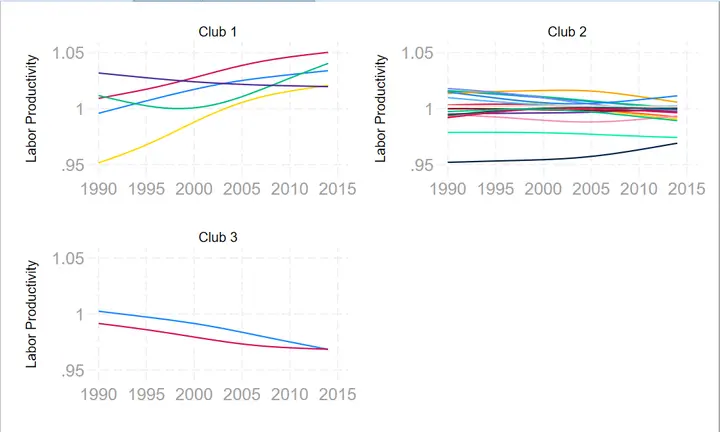
• $\boxed{\text{Club Convergence}}$ assumes that within economic groups with initially similar levels of economic development and among richer country groups, there is conditional convergence within each group, but no signs of convergence between the two groups.

$\sigma$-convergence:

• $\boxed{\sigma\text{-convergence}}$ assumes that the standard deviation $\sigma$ between different economies is constantly decreasing.

2. Convergence Speed

It seems like a mathematical concept from real analysis, but I first learned it in Romer’s “Advanced Macroeconomics,” so I’ve categorized it under economics.

I looked it up on Wikipedia (Rate of convergence), which is mainly applied in algorithm optimization and deep learning fields.

If a sequence $x_k$ converges to $L$, the expression $\mu$ is the rate of convergence.

$$ \lim_{k\to\infty}\frac{|x_{k+1}-L|}{|x_k-L|^q}=\mu $$

When $q=1$ in the equation, it is linear convergence, where the convergence speed is the ratio of the numerical difference to the convergence point between times $t$ and $t+1$.

Imagine a race. We measure speed by comparing the distance from the starting point.
Convergence is like anxiously waiting for the school bell. We care about how long it will take to reach the endpoint.

![Solow Model actually just added a factor on the horizontal axis](/img/收敛：从“算式的极限”到“增长的极限”.zh

IV. Econometric Analysis

1. Econometric Equations

(1) Absolute Convergence

Barro and Martin (1991)⁷ proposed the test equation for absolute $\beta$ convergence based on Baumol (1986)⁸.

$$ \small \frac{1}{T}\left[\log(y_{i,t+T}) - \log(y_{i,t})\right] = \alpha - \frac{(1 - e^{-\beta T})}{T} \log(y_{i,t}) + \varepsilon_i $$

Where $i$ represents the $i$th region, $t$ is the initial period, $t+T$ is the final period, $T$ is the length of the observation period, $y_{i,t}$ is the per capita GDP of region $i$ in period $t$, and $\beta$ represents the convergence speed. If $\beta > 0$, it indicates that the differences in economic development between regions will gradually disappear, eventually reaching the same steady state.

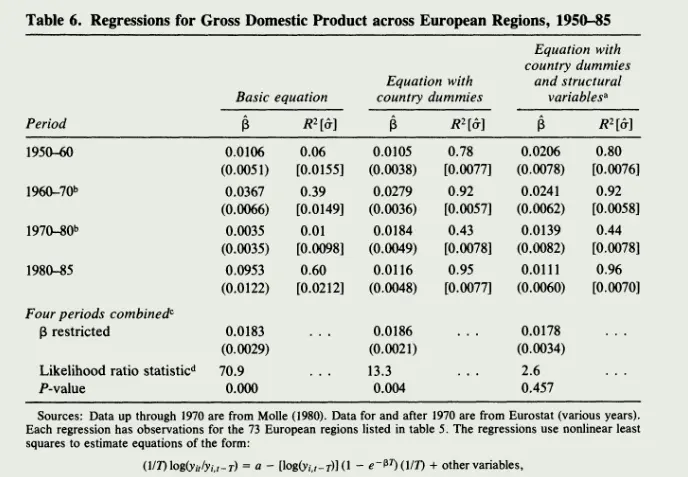
The above formula is derived from the neoclassical growth model (i.e., the Solow model).

Personally, I find that domestic descriptions of convergence regression variance are much clearer and more concise. Here, I refer to Peng Guohua (2005)⁹’s regression equation:

$$ g = c + \beta \ln y_0 + \varepsilon $$

Where $g$ is the growth rate, $c$ is the constant term, $y_0$ is the actual output, and $\varepsilon$ is the error term. When $\beta < 0$, it indicates that the growth rate $g$ is negatively correlated with the economic level $y_0$, consistent with our assumption that “high-level economies grow slower, while low-level economies grow faster.”

(2) Conditional Convergence

Barro and Martin (1992)¹⁰ proposed the test equation for conditional $\beta$ convergence based on the absolute $\beta$ convergence test equation:

$$ \small \frac{1}{T}\left[\log(y_{i,t+T}) - \log(y_{i,t})\right] = \alpha - \frac{(1 - e^{-\beta T})}{T} \log(y_{i,t}) + \lambda X_{i,t} + \varepsilon_{i,t} $$

The conclusions and parameter meanings are the same as those for absolute convergence, as conditional convergence implies that economic growth is related to the structural environment of the economy, hence the inclusion of $X_{i,t}$ as control variables.

The inconvenience of introducing control variables $X_{i,t}$ is that we have to study exogeneity again.

(3) Club Convergence

In groups with similar economic characteristics and similar growth paths, convergence exists within the group, but not between different economic groups. This phenomenon is called club convergence (Durlauf, 1995; Galor, 1996).

$$ \frac{1}{T}\left[\log(y_{i,t+T}) - \log(y_{i,t})\right] = \alpha + \beta \log(y_{i,t}) + \lambda D + \varepsilon_{i,t} $$

The variable meanings are the same as above, except that convergence is indicated only when $\beta < 0$, where $D_{i,t}$ is a dummy variable, i.e., grouping, such as all of East Asia following the same development path, or several cities developing as port cities.

An interesting study I found is modeling based on clustering criteria, such as using the “middle-income trap” as a clustering criterion¹¹.
Du (2017) (who is from Shandong University) introduced a Stata package to perform the econometric convergence test and club clustering algorithm by Phillips and Sul (2007)¹²¹³.
The grouping basis idea is roughly as follows:
$$ \lim_{x \rightarrow +\infty} \frac{X_j}{X_i} \rightarrow 1 $$ For detailed mathematical derivations, please click on the hyperlinks to their names.

Regarding club clustering operations in Stata, there are excellent tutorials available on YouTube and GitHub.

I have translated and added details to his do file:

Note: Use cd to adjust the Stata working environment (already noted in the do file comments)

BDY do file

dta file

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193

***************** This do file and accompanying data sources are from:
*  https://github.com/quarcs-lab/mendez2020-convergence-clubs-code-data
*  This file mainly translates part of the content and adds explanations for operations and details.

*-------------------------------------------------------
***************** Loading plotting packages*********************
*-------------------------------------------------------
* Install the convergence clubs package
findit st0503_1
net install st0503_1, from(http://www.stata-journal.com/software/sj19-1)
* Install package dependencies
ssc install moremata

* Reminder: Running these packages requires Stata 12 or above, and exporting results to Excel requires version 14.2 or above
*-------------------------------------------------------

*-------------------------------------------------------
clear all
macro drop _all
set more off
capture log close
*-------------------------------------------------------
***************** Define global macros for easy reference*********
*-------------------------------------------------------
* (1) Indicate the name of the dataset (Example: hiYes_log_lp.dta)
global dataSet hiYes_log_lp
* (2) Indicate the name of the variable to be studied (Example: log_lp)
global xVar log_lp
* (3) Write the label of the variable (Example: Labor Productivity)
global xVarLabel Labor Productivity
* (4) Indicate cross-sectional unit ID (Example: country)
global csUnitName country
* (5) Indicate temporal unit ID (Example: year)
global timeUnit year
*-------------------------------------------------------

// The logic for macro calls is to name the files in the Stata working directory
// Use cd to view and change the current working directory

cd F:\desktop\club convergence

*-------------------------------------------------------
***************** Load and set dataset  ***********
*-------------------------------------------------------
** Load data
use "${dataSet}.dta"

* Keep necessary variables
keep id ${csUnitName} ${timeUnit} ${xVar}

* Set panel data
xtset id ${timeUnit}
*-------------------------------------------------------


*-------------------------------------------------------
**** Run log-t convergence test, clustering, and merging algorithm, and list final results in table *****
*-------------------------------------------------------
* If we use a log file, all code and results will be recorded in the dataSet_clubs.txt file. Additionally, by using putexcel, we can export the results in table form to Excel.

* (1) Run log-t regression

putexcel set "${dataSet}_test.xlsx", sheet(logtTest) replace
// Set Excel as output file, default output to current working directory log you set (cd)

logtreg ${xVar}, kq(0.333)
// kq() is the weight of data to be discarded, default is 0.3
// The mathematical derivation of this command can be found at:
* https://www.stata-journal.com/article.html?article=st0503
* https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1468-0262.2007.00811.x
// Adding the following commands, the mathematical meaning is that within each cluster, as the limit is approached, the ratio of variables within the cluster tends to 1, indicating relative convergence

ereturn list
matrix result0 = e(res)
putexcel A1 = matrix(result0), names nformat("#.##") overwritefmt
// Command to import matrix

* (2) Run clustering algorithm
* Perform clustering to determine the number of clubs
putexcel set "${dataSet}_test.xlsx", sheet(initialClusters) modify
    psecta ${xVar}, name(${csUnitName}) kq(0.333) gen(club_${xVar})
matrix b=e(bm)
matrix t=e(tm)
matrix result1=(b \ t)
matlist result1, border(rows) rowtitle("log(t)") format(%9.3f) left(4)
putexcel A1 = matrix(result1), names nformat("#.##") overwritefmt

* (3) Run merging algorithm
* Merge clubs to determine comprehensive clubs, re-cluster
putexcel set "${dataSet}_test.xlsx", sheet(mergingClusters) modify
    scheckmerge ${xVar}, kq(0.333) club(club_${xVar})
matrix b=e(bm)
matrix t=e(tm)
matrix result2=(b \ t)
matlist result2, border(rows) rowtitle("log(t)") format(%9.3f) left(4)
putexcel A1 = matrix(result2), names nformat("#.##") overwritefmt

* (4) List final clusters
putexcel set "${dataSet}_test.xlsx", sheet(finalClusters) modify
    imergeclub ${xVar}, name(${csUnitName}) kq(0.333) club(club_${xVar}) gen(finalclub_${xVar})
matrix b=e(bm)
matrix t=e(tm)
matrix result3=(b \ t)
matlist result3, border(rows) rowtitle("log(t)") format(%9.3f) left(4)
putexcel A1 = matrix(result3), names nformat("#.##") overwritefmt

* In summary, regions have undergone two rounds of clustering grouping

*-------------------------------------------------------
*-------------------------------------------------------
***************** Generate relative variables**********
*-------------------------------------------------------
* Generate relative variables (for plotting)
* Group and take the average of each group, convenient for plotting each club later
save "temporary1.dta", replace
use "temporary1.dta"

collapse ${xVar}, by(${timeUnit})
gen id=999999
append using "temporary1.dta"
sort id ${timeUnit}

gen ${xVar}_av = ${xVar} if id==999999
bysort ${timeUnit} (${xVar}_av): replace ${xVar}_av = ${xVar}_av[1]
gen re_${xVar} = 1*(${xVar}/${xVar}_av)
label var re_${xVar} "Relative ${xVar} (Average=1)"
drop ${xVar}_av
sort id ${timeUnit}

drop if id == 999999
rm "temporary1.dta"

* Order variables
order ${csUnitName}, before(${timeUnit})
order id, before(${csUnitName})

* Export data to csv
export delimited using "${dataSet}_clubs.csv", replace
save "${dataSet}_clubs.dta", replace
*-------------------------------------------------------

*-------------------------------------------------------
***************** Plotting  *********************
*-------------------------------------------------------
** All lines

xtline re_${xVar}, overlay legend(off) scale(1.6) ytitle("${xVarLabel}", size(small)) yscale(lstyle(none)) ylabel(, noticks labcolor(gs10)) xscale(lstyle(none)) xlabel(, noticks labcolor(gs10)) xtitle("") name(allLines, replace)

graph save "${dataSet}_allLines.gph", replace
graph export "${dataSet}_allLines.pdf", replace

** Identified Clubs

summarize finalclub_${xVar}
return list
scalar numberOfClubs = r(max)

forval i=1/`numberOfClubs' {
    xtline re_${xVar} if finalclub_${xVar} == `i', overlay title("Club `i'", size(small)) legend(off) scale(1.5) yscale(lstyle(none)) ytitle("${xVarLabel}", size(small)) ylabel(, noticks labcolor(gs10)) xtitle("") xscale(lstyle(none)) xlabel(, noticks labcolor(gs10)) name(club`i', replace)
    local graphs `graphs' club`i'
}
graph combine `graphs', ycommon
graph save "${dataSet}_clubsLines.gph", replace
graph export "${dataSet}_clubsLines.pdf", replace

** Within-club averages

collapse (mean) re_${xVar}, by(finalclub_${xVar} ${timeUnit})
xtset finalclub_${xVar} ${timeUnit}
rename finalclub_${xVar} Club
xtline re_${xVar}, overlay scale(1.6) ytitle("${xVarLabel}", size(small)) yscale(lstyle(none)) ylabel(, noticks labcolor(gs10)) xscale(lstyle(none)) xlabel(, noticks labcolor(gs10)) xtitle("") name(clubsAverages, replace)

graph save "${dataSet}_clubsAverages.gph", replace
graph export "${dataSet}_clubsAverages.pdf", replace

clear
use "${dataSet}_clubs.dta"

*-------------------------------------------------------

*-------------------------------------------------------
***************** Export list of clubs  ****************
*-------------------------------------------------------
* The following code exports the country list and club membership to a .csv file. This list can be used as a convenient reference in the appendices of publications.

summarize ${timeUnit}
scalar finalYear = r(max)
keep if ${timeUnit} == `finalYear'

keep id ${csUnitName} finalclub_${xVar}
sort finalclub_${xVar} ${csUnitName}
export delimited using "${dataSet}_clubsList.csv", replace
*-------------------------------------------------------

2. Empirical Results (Examples)

China’s current empirical results basically satisfy $\sigma$ convergence¹⁴ and club convergence (classification is generally regional, such as eastern, central, and western regions)¹⁵. The standards of GDP, total factors, and industrial output basically lead to the same conclusions¹⁶.