因果效应

2017 年 Angrist 凭借计量因果推断的贡献获得诺奖，其后双重差分方法大行其道。计量经济学宣扬自己研究的是因果关系而非相关关系。这里要介绍的就是“潜在结果”框架下的因果效应。本文学习记录的原因是听了《世界经济》手把手第二期讲座。听了刘若鸿老师《工业用地价格与企业产能利用率》¹ 论文分享后决定整理学习因果效应。

因果框架有哪些？

今因果框架众多，群雄并起，统计学（本家之外，药物学、心理学也各有自家统计理解）、经济学、计算机皆有流派，交错纵横，我也不清楚整个体系到底如何。

个人接触比较多的是 Judea Pearl 的结构因果模型（Structural Causal Model, 简称 SCM）。对于他的著作《为什么》² ，我个人理解是，关联-干预-反事实就是三个因果层级。工具变量的选用就是控制后门（保证唯一的外生影响），控制变量的设置就是控制前门。

ATE、ATT、ITT、LATE 这部分知识在《基本无害的计量经济学》² 中零散出现。整个框架是基于 Donald Rubin 提出的潜在结果框架(Potential Outcome Framework ，也叫 Rubin Causal Model，简称 RCM)。

有趣的是，Judea Pearl（在《为什么》中）提出因果路径下的反事实就是 Rubin 提出的"潜在结果"，不过 Rubin 回应两者完全不是一回事³，并且不赞成路径图的分析方法。 （个人不太能理解 rubin 的回应，在我个人看来 SCM 的路径箭头方向对应的就是 RCM 的加减符号方向）。

据我所知，目前因果分析在统计学中还分为频率学派、贝叶斯学派，研究通过马尔科夫链去理解因果推断。这方面个人就完全知之甚少了。个人对这块知识的了解完全来自于 B 站 up——Fmajor 的科普视频。

细说 RCM 因果效应

ATE、ATT、ITT、LATE 是不同的统计估计量。

引言：社会科学和自然科学面临的统计难题

社会科学和自然科学的统计学面临不同的挑战。对于物理学家、生物学家来说，他们不用在意无偏性——因为大部分自然科学的实验都可以轻而易举地找到对照组和实验组。

经济学并非如此，经济学的统计学尤其在意大数定理、中心极限定理、渐近性。由于社会科学测量的政策效应、经济因素的影响很难像物理规律一样推广，数据收集和测量已经是难题，代表性、泛用性在这之上更是一个大难题。

老人群体得到的数据不一定对青少年有效；美国数据得到的结论不一定对中国有效；明年的数据得到的结论不一定对今年的社会有效……

需要明确的是——在这种情况下，计量只是妥协性给出一种可信性革命的方法。而什么样的方法才能真正得到社会科学的因果关系，这是一个永无止境的难题，也是因果推断永恒魅力所在。

从 ATE 到 ATT

从小学开始，我们就接触了使用各个数组的均值来进行比较分析。不过这种分组对比只是因果讨论的起点，需要进一步对这种分组差异进行分解，进而探讨因果关系。

在 OLS 中，控制变量的思想含义可以通过 FWL 定理理解——保持其他变量不变。当解释变量为 01 二元变量时，就类似实验组和对照组的划分。

计量最在意的，想要求得的变量是平均处理效应——如平行宇宙般完美的实验组和对照组。

$\boxed{平均处理效应}$ （average treatment effect，简称 ATE）：直接用两组数据均值之差作为估计量。既可以看作总体均值相减，又可以看作分组相减的均值（例如双胞胎数据估计）：

$$\bar Y_1-\bar Y_0=\sum_{i=1}^{N_1}\frac{Y_{i}(1)}{N_1}-\sum_{i=1}^{N_0}\frac{Y_{i}(0)}{N_0}$$

将 $D_i$ 视为处理行为。 $D_i$ 为 1 为实验组，为 0 为对照组。产生线性方程如下：

$$\begin{align}Y_{i}&=\begin{cases} Y_{1i} \quad if D_i = 1 \newline Y_{0i} \quad if D_i = 0 \end{cases} \newline &=Y_{0i}+(Y_{1i}-Y_{0i})D_{i} \end{align}$$

例如自然科学的对照组实验组，数据一减就相当于整体的 ATE 。

社会科学也想如此，但有很多问题，只能退而求其次：

分组相减，可得如下式子（注意红色部分）：

$$\begin{aligned} &\mathbf{E}[Y_{i}\mid D_{i}=1]-\mathbf{E}[Y_{i}\mid D_{i}=0]\newline& =\color{red}{\underbrace{\mathbf{E}\lfloor Y_{1i}\mid D_{i}=1\rfloor-\mathbf{E}[Y_{0i}\mid D_{i}=1]}_{\text{处理的平均处理效应ATT}} } \newline &+\underbrace{\mathbf{E}[Y_{0i}\mid D_{i}=1]-\mathbf{E}[Y_{0i}\mid D_{i}=0]}_{偏误} \end{aligned}$$

其中 $\mathbf{E}[Y_{0i}\mid D_{i}=1]$ 是我们主动添加的，是想要却无法直接找到的另一个”平行宇宙“——假如$\mathbf{E}[Y_{\color{blue}{1i}}\mid D_{i}=1]$ 部分群体，在平行世界没有没有接受处理，他们的状态表示为 $\mathbf{E}[Y_{\color{blue}{0i}}\mid D_{i}=1]$, 也就是 Rubin 想找到的"潜在结果"。

$\color{red}{\mathbf{E}\lfloor Y_{1i}\mid D_{i}=1\rfloor-\mathbf{E}[Y_{0i}\mid D_{i}=1]}$ 代表着 $\boxed{处理组平均处理效应}$（Average Treatment Effect on Treated，简称 ATT）。

同理，$\mathbf{E}\lfloor Y_{1i}\mid D_{i}=0\rfloor-\mathbf{E}[Y_{0i}\mid D_{i}=0]$ 代表 $\boxed{对照组平均处理效应}$ （Average Treatment Effect on Untreated，简称ATU）。采用同样的构造，构造出新的平行宇宙情况

$$ \begin{aligned}
&\mathbf{E}[Y_{i}\mid D_{i}=1]-\mathbf{E}[Y_{i}\mid D_{i}=0]\\ & ={\underbrace{\mathbf{E}\lfloor Y_{1i}\mid D_{i}=0\rfloor-\mathbf{E}[Y_{0i}\mid D_{i}=0]}_{\text{对照组的平均处理效应ATU}} }\\ &+\underbrace{\operatorname{E}[Y_{1i}\mid D_{i}=1]-\operatorname{E}[Y_{1i}\mid D_{i}=0]}_{\operatorname*{\text{选择性偏误}}} \end{aligned}\\ $$

再没有比“一个二项选择分裂出两个平行宇宙”更好的对照试验了，然而没有人能真正获得这种数据！因此，经济学家的做法是想通过 ATE 来估计 ATT，于是引入了随机试验（RCT）。

强调——实际上我们最想知道的一直是ATE（真正的实验组和对照组），但是我们只能观测到政策冲击推行以后的数据，因此才想从局部效应（ATT、ATU）推及到ATE。因此反事实也可以被看作修补出“缺失的数据”。

也就是说，ATT 和 ATU 都是局部群体，并不是计量的终极目标—— ATE（整体）。

RCT：让 ATT 趋近 ATE

RCT 全称为 Randomized controlled trial，代表 $\boxed{随机试验}$，在随机试验条件下，ATE=ATT，接下来展开介绍：

平行世界分裂出的这部分群体 $\mathbf{E}[Y_{0i}\mid D_{i}=1]$ 和现实一开始就没有接受过处理的群体 $\operatorname{E}[Y_{0i}\mid D_{i}=0]$ 相减，如果不为 0，就产生了选择性偏差。

原因可能是样本选择偏差：例如我们做健身相关的调查，但只去健身馆收集数据，肯定不能实现有效对比；例如美军著名的飞机幸存者偏差，飞回来的飞机是活下来的飞机，通过他们身上的损伤估计需要加强的部位也是不可靠的；

也可能是自选择偏差：例如入学性别比不均不代表歧视，因为这种分析忽略了性别比的申请倾向，某种性别的人更倾向于申请难度更高的，淘汰率也就更高；警察执法更关注某个种族也不代表就是歧视，看看那个种族犯罪频率是不是相对就高一些。

也可以理解为个体差异，例如药物实验对老人、中年人、小孩的效应其实是不同等。一些人上网课效果更高，而另外一些人上网课效果更差。我们想估计是全部群体的平均效应，不想偏向某个局部群体。

遗漏变量、模型错误、测量错误、样本不足都可能导致。

如果我们采用随机试验的方法，样本是随机分布的。我们希望这种随机试验能把一些我们没观察到的影响变量给平均掉，进而使得 $D_i$ 和 $Y_{0i}$ 具有独立性，这意味着 $\mathbf{E}[Y_{0i}\mid D_{i}=1]=\mathbf{E}[Y_{0i}\mid D_{i}=0]=\mathbf{E}[Y_{0i}]$。

此时 ATE 估计得到了有效的简化：

$$\begin{aligned} &\mathbf{E}[Y_{1i}\mid D_{i}=1]-\mathbf{E}[Y_{0i}\mid D_{i}=1]\newline&=ATT =\mathbf{E}[\mathbf{Y}_{1i}-\mathbf{Y}_{0i}\mid D_{i}=1] \newline &=ATE=\mathbf{E}[Y_{1i}-Y_{0i}] \end{aligned}$$

进一步通过回归式子来估计：

$$\begin{align}Y_{i}&=\begin{cases} Y_{1i} \quad if D_i = 1 \newline Y_{0i} \quad if D_i = 0 \end{cases} \newline &=Y_{0i}+(Y_{1i}-Y_{0i})D_{i} \newline & =\alpha+\rho D_i+\eta_i \end{align}$$

由于

$$\begin{aligned}&\operatorname{\mathbf{E}}[Y_i\mid D_i=1]=\alpha+\rho+\operatorname{\mathbf{E}}[\eta_i\mid D_i=1]\newline &\operatorname{\mathbf{E}}[Y_i\mid D_i=0]=\alpha+\operatorname{\mathbf{E}}[\eta_i\mid D_i=0]\end{aligned}$$

可以得到两者相减

$$\begin{aligned}&\operatorname{\mathbf{E}}[Y_i\mid D_i=1]-\operatorname{\mathbf{E}}[Y_i\mid D_i=0]\newline &=\underbrace{\rho}_\text{处理效应}+\underbrace{\operatorname{\mathbf{E}}[\eta_i\mid D_i=1]-\operatorname{\mathbf{E}}[\eta_i\mid D_i=0]}_\text{选择性偏误}\end{aligned}$$

选择偏差 $\eta_i\ne0$ 时，意味着残差和 $D_i$ 相关。我们强调随机试验，就是希望随机干预试验能够使得二者无关，消除这种选择偏差。所以当满足随机试验时，$\eta_i=0$, $ATE\xrightarrow{RCT}ATT$。

这也告诉了我们为什么要重视残差分析。

补充——卢卡斯批判

政策随机性的一种体现是人们对政策的预期是一致的。而诺奖得主卢卡斯曾经有一个著名的观点：当政策实施以后，人们对政策就有了预期，这时候再把政策当成外生冲击是不合适的。预期应当被纳入决策分析。

从 ITT 到 LATE

RCT 在意的是政策的外生性，但即便政策是外生的，人们对政策的反应也可能是内生的。

$\boxed{意向性分析}$（Intention to treat，简称 ITT）。虽然随机干预试验很有用，但我们要研究的变量不总是随机分布的。例如刘若鸿老师的《工业用地价格与企业产能利用率》——研究工业用地集聚在某一档土地等级周围。此时买家们不讲武德，是有备而来，也就不是随机分布的。此时我们考虑其他随机分布的变量会影响他们的决策。

先使用 SCM 的路径图来理解会更加形象：

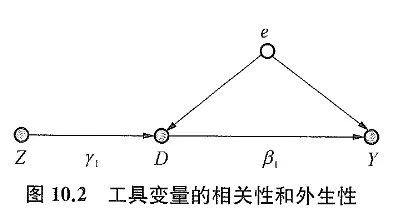
再举例 Angrist（2011）⁴的一篇论文，研究参加越南战争对收入的影响，里面参军变量不好使，就使用了入伍资格作为工具变量。（怀念短短 6 页的计量论文时代）

显然，存在这样一个过程，一个人先被告知有没有入伍资格，然后他决定是否进入军队。

ITT 式子如下所示：

$$ITT=\mathbf{E}[Y_i|Z_i=1]-\mathbf{E}[Y_i|Z_i=0]$$

可以看出 ITT 估计和 $\mathbf{E}[Y_{i}\mid D_{i}=1]-\mathbf{E}[Y_{i}\mid D_{i}=0]$ 相当类似，也就是说，当 $D_i$ 和 $Z_i$ 一一对应时，也就是 $z=d$ 时，ITT=ATE。

• $\pi_N$: 无论我有没有资格，我最终都不会参军。
• $\pi_D$: 逆反心态，有参军资格我偏不去，没有参军资格我偏要去。
• $\pi_A$: 无论我有没有资格，我最终都会去参军。
• $\pi_C$: 服从安排，有资格我就去，没资格我就不去。

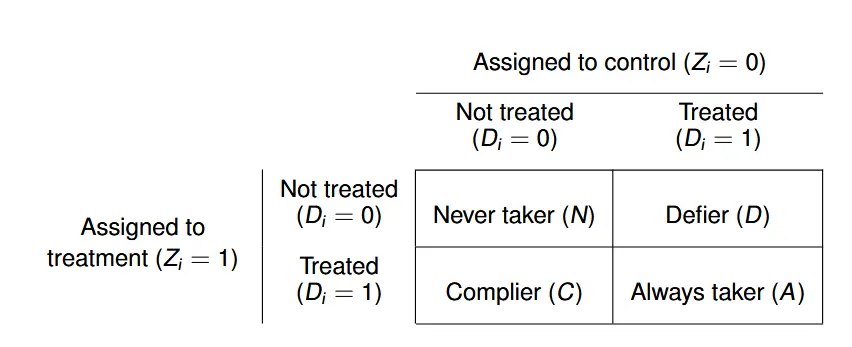
同时由于我们本来就是基于军人样本进行统计， $D_i$ 并非随机分布，因此只有如下式子：

$$\begin{aligned} \mathbf{E}[D_i=1|Z_i=0]=\pi_A+\pi_D\newline \mathbf{E}[D_i=1|Z_i=1]=\pi_A+\pi_C \end{aligned}$$

如此一来肯定不能单独估计出 $\pi_i(i\in{A,C,D,N})$ 了。

不过由于随机分布，结果会成比例，可以变形出线性方程：

$$ITT=\pi_CITT_C+\pi_AITT_A+\pi_NITT_N+\pi_DITT_D$$

实际上，如果知道每个人对待抽签的反应，我们是可以计算所有 $π_i$ 的值的，但是计量要解决的恰恰是我们不知道总体样本点分布，因此做出假设：

解决办法是增加假设 ——很有经济学笑话味道了。插入笑话原文：一个物理学家、一个化学家和一个经济学家漂流到孤岛上，十分饥饿。这时海面上漂來一个罐头。物理学家说：“我们可以用岩石对罐头施以动量，使其表层疲劳而断裂。”化学家说：“我们可以生火，然后把罐头加热，使它膨胀以至破裂。”经济学家则说：“假设我们有一个开罐头的起子……。”

加入假设后，我们就直接得到了 LATE：

$$\mathrm{LATE}=\mathrm{CATE}_{\mathcal{C}}=\frac{\mathrm{ITT}}{\pi_{\mathcal{C}}}$$

此时估计如下：

$$\small \hat{\mathbf{CATE}_C}=\frac{\mathbf{E}\Big[Y_i|Z_i=1\Big]-\mathbf{E}\Big[Y_i|Z_i=0\Big]}{\mathbf{E}\Big[D_i|Z_i=1\Big]-\mathbf{E}\Big[D_i|Z_i=0\Big]}=\frac{\mathrm{effect~of~}Z_i\text{ on }Y_i}{\mathrm{effect~of~}Z_i\text{ on }D_i}=\frac{\operatorname{ITT}_Y}{\operatorname{ITT}_D}$$ 其实就是工具变量中的估计式子

$$\beta^{IV}=[E(Z^\prime Z)−E(Z^\prime X)]^{-1}[E(Z^\prime Z)−E(Z^\prime Y)]$$ 矩阵表示含义—— X先对Z做回归，然后Y对Z做回归。

所以也可以理解工具变量其实对样本添加了权重，越满足假设和工具变量相关的样本权重越高。

LATE 部分重点参考了牛津的课件，如果想看相对代数化的说明可以参考哈佛的课件和《基本无害的计量经济学》。

数理经济中的社科属性？

直接说"解决办法是添加几个假设"未免有些太经济学地狱笑话了。从经济含义看更加直观，如果我们研究的政策足够独特，我们需要论述政策对每个人都有影响，也就是假设中的单调性。在使用工具变量时，也需要介绍工具变量和解释变量之间的社会关系。所以为何经济学计量区别于数学？这些假设就是对社会现象的描述总结，就是其社科属性的鲜明体现。

比如我们的样本是医院样本——一般来说，没有病人不会去跟医生反着来；还比如我们的样本是政府政策，由于政府的强硬手段，没人能够跟政府反着来，因此确实其他反应就为0，大家都是顺从的反应。

当然，实际上工具变量还是会有偏差（一般会增大估计量），所以要仔细理解自己选择的工具变量和 y 和 x 的关系。

最近学习高级宏观也有所体悟。高宏的方法非常单调，变分法加拉格朗日基本解决了所有经典模型的最优化。难点在于每个高宏模型飞来飞去的假设条件和阴间变形。无论是公式变形还是突然施加的假设，都是提炼经济现象的一个特征，然后加以数学化，这才是最大的难点。例如知识生产函数（知识作为全要素）、科夫道格拉斯生产函数（规模报酬）、家庭约束（消费贴现小于财富贴现）、家庭效用函数（风险规避）。

我开始认为——以怎样的框架挖掘均衡；通过经济现象构建具有特性的函数；总结出最优化约束条件才是经济学区别数理复合人才的“经济思想与直觉”。

顺便插入下高宏笔记。

总结

进一步举例子说明，DID 估计是 ATE；RDD 估计是 LATE ；聚束分析是 LATE。

ATE 和 LATE 是我们所求的，是我们渴望平行世界那样完善的对照试验，但我们有的只是 ATT 和 ITT。

当 D 满足 RCT 时，ATT=ATE。

当 D 不满足 RCT，但 Z 满足时，同时基于单调性和限制约束造出工具变量 (IV）或者 RDD，此时 ITT=LATE。

当 D 不满足 RCT，Z 也找不到时，就采用其他方法估计反事实情况，例如群聚分析 (通过残差分析变形直接估计反事实的分布和当前集聚现象形成对比)、合成控制……

教材一般也会引入匹配论来实现这些估计假设。

综上，计量模型就是基于这样的潜在结果框架分析因果关系，宣扬自己研究的是因果科学。

如此一看，是否颇有"无中生有",“由果索因"之妙也？