原神概率论：材料合成天赋选 10%双倍还是 25%返还？

网上计算数学期望的已经有很多，但是似乎没人计算方差，这里把方差计算补上。

一、设定介绍

在原神中，三个低级材料能够合成一个高级材料。我们表示为 $a \xrightarrow{\text{转化}}\dfrac{b}{3}$

为保持单位一致，我们统一使用 b 表示投入与产出，假设两边同时有初始材料 a，也就等价于 $\dfrac{b}{3}$。

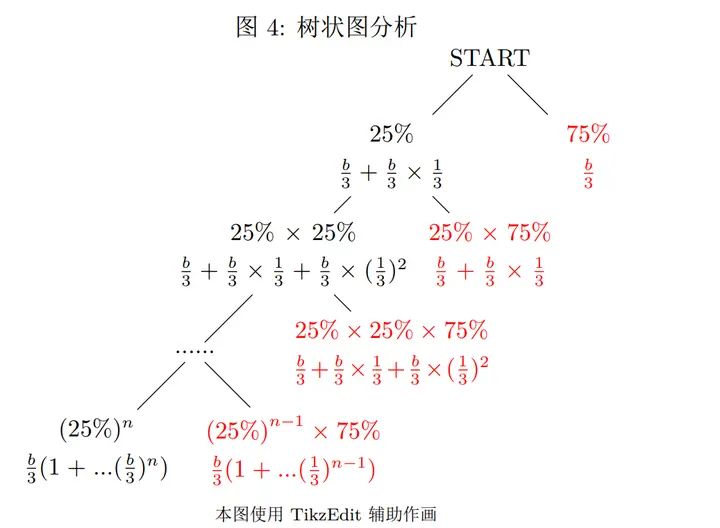
此时有两种天赋，如下图

• 一种是有 10%的概率双倍产出。

每使用 a 个材料，也就是 $\dfrac{b}{3}$ 材料时，10%概率直接产出 $\dfrac{2}{3}b$ 材料。

• 一种是有 25%的概率返还部分低级材料。

每使用 a 个材料，也就是 $\dfrac{b}{3}$ 材料时，25%概率返回 $\dfrac{1}{3} \times \dfrac{1}{4}b$ 材料。

使用随机变量的形式，也就是：

$$X_{总产出}=\frac{b}{3}+Y_{额外产出}$$

二、计算期望与方差

网上计算数学期望的已经有很多，但是似乎没有人计算方差，这里顺便把方差的计算补上。

（一）10%双倍产出的期望与方差

1、期望

此时就是二项分布离散分布列 。10% 概率双倍产出，90% 概率普通产出。

如下表 1：

$$ \mathrm{E}_{{双倍}}[X]=\mathrm{E}_{{双倍}}[\frac{b}{3}+Y_{额外}]=\frac{b}{3}+np=10% \times\frac{2}{3}b+90% \times\frac{1}{3}b $$ 所以投入 a 材料，等价于投入 $\dfrac{b}{3}$ 材料，10%双倍天赋的数学期望 $E_{\text{双倍}}(\dfrac{b}{3})=\dfrac{11 b}{30} $ 。

2、方差

$$ \mathrm{Var}[X]=\mathrm{Var}[\frac{b}{3}+Y_{额外产出}]=\mathrm{Var}[Y_{额外产出}] $$

$$ \mathrm{Var}[Y]=np(1-p)=\frac{b}{3}\times0.1\times0.9=\frac{3}{100}b $$ 所以投入 a 材料，等价于投入 $\dfrac{b}{3}$ 材料，10%双倍天赋的方差 $Var_{\text{双倍}}(\dfrac{b}{3})=\dfrac{1}{100}b^2$。

（二）25%返回材料的期望与方差

1、期望的两种算法

方法一：等比数列

$$ \begin{align*} E_{\text{返回}}\left(\frac{b}{3}\right)
&= \frac{b}{3} + \frac{b}{3} \times 25\% \times \frac{1}{3} + \ldots + \frac{b}{3} \times \left(\frac{1}{12}\right)^n \newline &= \frac{b}{3} \times (1+{\frac{1}{12}}+{\frac{1}{12}}^2+…+{\frac{1}{12}}^n) \newline &= \frac{b}{3} \times \frac{1 \times (1-{\frac{1}{12}}^n)}{1-\frac{1}{12}} \newline \end{align*} $$

$$ \lim_{n\rightarrow + \infty}E_{\text{返回}}\left(\frac{b}{3}\right)=\frac{b}{3} \times \frac{1 \times (1-{\frac{1}{12}}^n)}{1-\frac{1}{12}}=\frac{4b}{11} $$

展示图如下：

我们可以验证下这种分类是否讨论完了所有情况，将所有概率加总：

$$ \lim_{n\rightarrow +\infty}75\%+…+{(25\%)}^{n-1}75\%=1 $$ 所有对应概率加总为 1，一定程度上验证了这种分类的正确性。

方法二：递归

由于返还后的材料继续炼丹，会形成一个递归，因此我们得到： $$ E_{\text{返回}}\left(\frac{b}{3}\right)=\frac{b}{3} +E_{\text{返回}}\left(\frac{b}{3}\right)\times 25% \times \frac{1}{3} $$ 答案与上面相同：

所以投入 a 材料，等价于投入 $\dfrac{b}{3}$ 材料，25%返回天赋的数学期望 $E_{\text{返回}}(\frac{b}{3} )=\frac{4b}{11}$。

2、方差

以下方差计算思路来自 《【原神】关于材料合成天赋选 10% 双倍还是 25% 返还的更精细计算》

此时继续引入递推关系，我们有如下递推关系。

$$\mathrm{E}(a_k)=\mathrm{E}(a_{k-1})\times 25% \times \dfrac{1}{3}$$

含义：

第 $k$ 次合成前，手中有 $a_k$ 个初级材料。

能进行第 $k$ 次合成的条件是： 第 $k-1$ 次合成触发效果返还了部分初级材料。

使用条件期望的描述也就是

$$ \mathrm{E}(a_k)=\mathrm{E}[\mathrm{E}[a_k| a_{k-1}]]=\mathrm{E}[\frac{1}{12}a_{k-1}]=\frac{1}{12}\mathrm{E}[a_{k-1}] $$

$$ \mathrm{E}[X]=\sum_1^{k}a_k=\sum_1^{k}\frac{1}{12^k}a_0 $$

这个式子可以展开为递归，也可以展开为等比数列，也就是前面计算期望的两种方法。

引入完条件期望后，接下来引入方差分解公式：

$$ \mathrm{Var}[X]=\mathrm{E}[X^2]-[\mathrm{E}(X)]^2 $$ 变形加入条件期望，变形可以得到两个式子 $\mathrm{E}(X|Y)$。

$$ \mathrm{Var}[\mathrm{E}(X|Y)]=\mathrm{E}\left\{\left[\mathrm{E}(X|Y)\right]^{2}\right\}-\left\{\mathrm{E}\left[\mathrm{E}(X|Y)\right]\right\}^{2}=\mathrm{E}\left\{\left[\mathrm{E}(X|Y)\right]^{2}\right\}-\left[\mathrm{E}(X)\right]^{2} $$

$$ \mathrm{E}[\mathrm{Var}(X|Y)]=\mathrm{E}\left\{\mathrm{E}(X^{2}|Y)-[\mathrm{E}(X|Y)]^{2}\right\}=\mathrm{E}(X^2)-\mathrm{E}\left\{\left[\mathrm{E}(X|Y)\right]^2\right\} $$

上面两个式子相加得到方差分解公式：

$$ \mathrm{Var}(X)=\mathrm{Var}[\mathrm{E}(X|Y)]+\mathrm{E}[\mathrm{Var}(X|Y)] $$

将这个式子代入 $a_k、a_{k-1}$。

$$ \mathrm{Var}(a_k)=\mathrm{Var}[\mathrm{E}(a_k|a_{{k-1}})]+\mathrm{E}[\mathrm{Var}(a_k|a_{k-1})] $$ 其中

$$ \mathrm{Var}[\mathrm{E}(a_k|a_{{k-1}})]=\mathrm{Var}[\frac{1}{12}a_{k-1}] $$ $$ \mathrm{E}[\mathrm{Var}(a_k|a_{k-1})]=\mathrm{E}[np(1-p)]=\mathrm{E}[np(1-p)]=\mathrm{E}\left[\frac{a_{k-1}}{16}\right] $$ 得到：

$$ \begin{aligned}\mathrm{Var}\left[a_k\right]=\frac{3}{4} \frac{a_0}{12^k}+\frac{1}{12^2} \mathrm{Var}\left[a_{k-1}\right]\end{aligned} $$ 因为 $\mathrm{Var}(a_0)=0$ ,使用递归，可以得到通项公式

丢给 GPT 算了然后验证了一下，也满足方差项之间144倍关系：

$$ \mathrm{Var}[a_k]=\frac{9}{143}a_0\left(1-\frac{1}{144^k}\right)=a_0\times \frac{1}{16\times 144^{k-1}} $$ $$ \mathrm{E}\left[a_k^2\right] = \mathrm{Var}[a_k] + \left(\mathrm{E}\left[a_k\right]\right)^2 =9\frac{k{a_0}}{12^{2k}} + \frac{a_0^2}{12^{2k}} $$

又设置之后递归融合$ l $次

$$ \begin{aligned} &\mathrm{E}\left[a_k a_\ell\right]=\mathrm{E}\left[\mathrm{E}\left[a_k a_\ell \mid a_\ell\right]\right]\\ &=\mathrm{E}\left[a_\ell \mathrm{E}\left[a_k \mid a_\ell\right]\right]\\ &=\frac{1}{12^{k-\ell}}\mathrm{E}\left[a_\ell^2\right]\\ &=\frac{9a_0^2l+a_0^2}{12^{k+\ell}} \end{aligned} $$ 这是为了计算协方差：

$$ \mathrm{Cov}(a_\ell, a_k) = \mathrm{E}\left[a_\ell a_k\right] - \mathrm{E}\left[a_\ell\right]\mathrm{E}\left[a_k\right]=\frac{9a_0^2\ell}{12^{k+\ell}} $$ 代入计算方差：

因为原神是三个合成一个:

$$ X_n=\sum\limits_{k=0}^n \frac{a_k}{3} $$ 得到方差计算公式：

$$ \mathrm{Var}\left[X_n\right] =\frac{1}{9}\left(\sum_{k=0}^n \mathrm{Var}\left[a_k\right]+2 \sum_{\ell<k} \mathrm{Cov}\left[a_{\ell} a_k\right]\right) $$

代入得到：

以下部分是 GPT 展开的，我能感觉到问题出现在方差累加那部分，不可能出现无法消除的一个1的单独项，这样就无法收敛了.

$$ \begin{align*} \text{Var}[X_n] &= \frac{1}{9} \Bigg( \frac{9}{143} a_0 \left[ (n+1) - \frac{144}{143} \left( 1 - \frac{1}{144^{n+1}} \right) \right] \\&\quad + 2 \cdot \frac{9a_0^2}{11} \sum_{\ell=0}^{n-1} \frac{\ell}{12^{2\ell}} \left( 1 - \frac{1}{12^{n-\ell}} \right) \Bigg) \end{align*} $$接下来让n趋于极限。

按照代码图，目测估计下极限应该是 0.009b 附近，也就是 0.027a 附近。

三、结论与计算机模拟

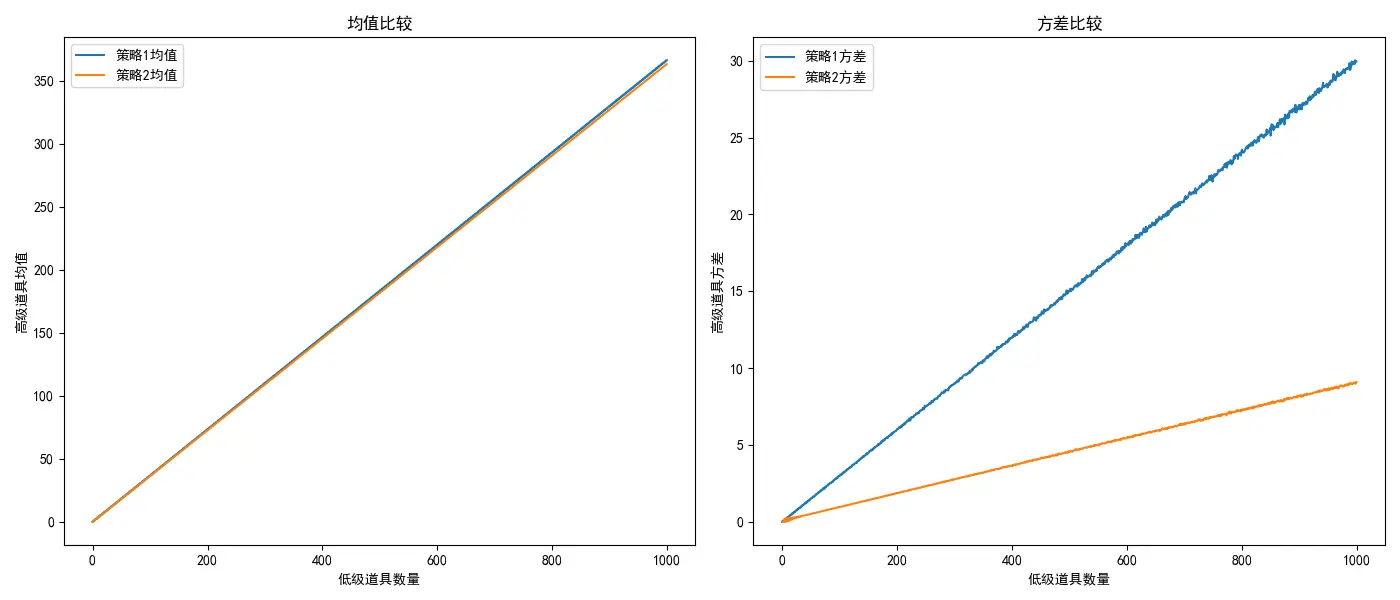
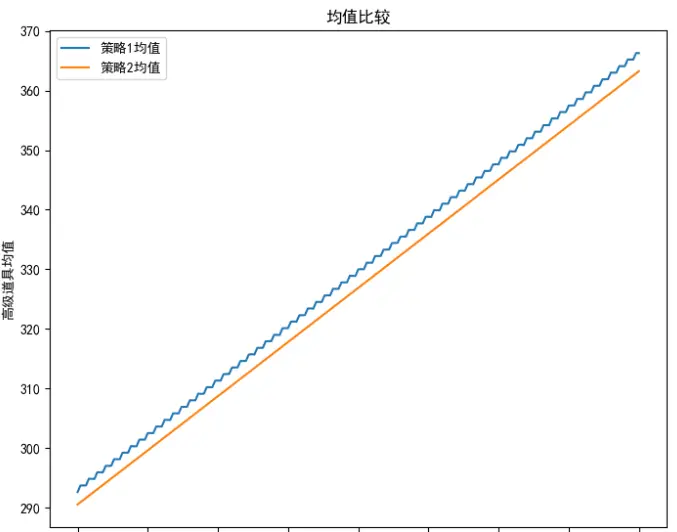
使用代码拟合一下,也是和计算结果吻合的：

• 10%期望略微高一些，但是期望差异1000个材料以内并不大。
• 25%的方差波动更小，只是次数增多，摩拉成本会多一点。
• 考虑到原神素材999的上限，高级材料期望也就相差2-3个左右。

实验代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87

import random
import matplotlib.pyplot as plt
import numpy as np

# 设置matplotlib的字体，以便支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 模拟合成高级道具的函数
def synthesize_items(low_items, strategy):
    high_items = 0
    while low_items >= 3:
        合成结果 = random.random()
        if strategy == 1:
            if 合成结果 < 0.1:
                high_items += 2  # 额外获得一个高级道具
            else:
                high_items += 1
        elif strategy == 2:
            if 合成结果 < 0.25:
                low_items += 1  # 返还一个低级道具
            high_items += 1
        low_items -= 3
    return low_items, high_items

# 模拟多次合成并计算平均收益和方差
def simulate_synthesis(low_items, strategy, trials=10000):
    results = []
    for _ in range(trials):
        _, high_items = synthesize_items(low_items, strategy)
        results.append(high_items)
    mean = np.mean(results)
    variance = np.var(results)
    return mean, variance

# 绘制图表
def plot_results(means, variances, strategies):
    plt.figure(figsize=(14, 6))

    # 绘制均值比较图
    plt.subplot(1, 2, 1)
    for strategy, data in means.items():
        plt.plot(data, label=f'策略{strategy}均值')
    plt.xlabel('低级道具数量')
    plt.ylabel('高级道具均值')
    plt.title('均值比较')
    plt.legend()

    # 绘制方差比较图
    plt.subplot(1, 2, 2)
    for strategy, data in variances.items():
        plt.plot(data, label=f'策略{strategy}方差')
    plt.xlabel('低级道具数量')
    plt.ylabel('高级道具方差')
    plt.title('方差比较')
    plt.legend()

    plt.tight_layout()
    plt.savefig('results.png')  # 保存图表为图片文件

# 主函数
def main():
    num_items = range(1, 1001)  # 投入的低级道具数量范围
    trials = 100000  # 模拟次数
    strategy1_means = []
    strategy1_variances = []
    strategy2_means = []
    strategy2_variances = []

    for items in num_items:
        mean1, variance1 = simulate_synthesis(items, 1, trials)
        mean2, variance2 = simulate_synthesis(items, 2, trials)
        strategy1_means.append(mean1)
        strategy1_variances.append(variance1)
        strategy2_means.append(mean2)
        strategy2_variances.append(variance2)

    plot_results({
        1: strategy1_means,
        2: strategy2_means
    }, {
        1: strategy1_variances,
        2: strategy2_variances
    }, [1, 2])

if __name__ == '__main__':
    main()

更多讨论详见：原神概率论