解释“潮玩热”:从网络效应到多重均衡

“人是政治的动物,但人心不可轻易揣测。”——亚里士多德
泡泡玛特产品的典型事实
在泡泡玛特的商业构想中,潮玩经济应该率先在发达国家出现。
经济理论非常简单:
消费分为生存性和发展性,发展性消费只有在满足了生存性消费的情况下才能满足。
然而实际情况是——亚洲发展中国家对潮玩的市场反应比发达国家更加迅速。
- 从微观来看,一个人愿意为谷子经济紧衣缩食;
- 从宏观来看,目前社会消费升级伴随着生育率日渐走低1。
反应到具体函数上,泡泡玛特这类商品的典型事实是:
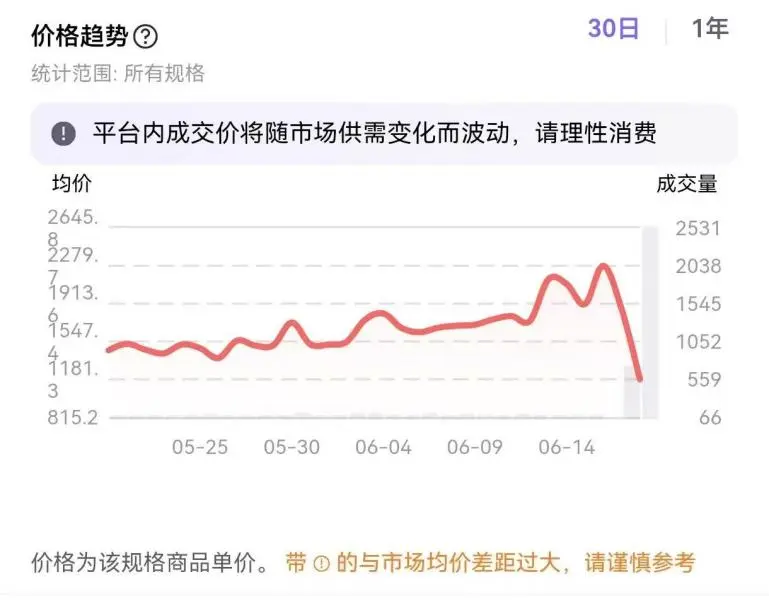
供不应求时,价格(至少是官方价格)基本不变,同时泡泡玛特的黄牛价格在最近遭遇下滑(2025 年 7 月左右)。
这意味着,
- 首先泡泡玛特不是吉芬商品2,因为其定价不菲,定义为发展性消费,并非低档品。
- 不能用凯恩斯理论出发的价格粘性解释,因为这里没有工会参与,菜单成本也很低。
- 泡泡玛特的官方往往不怎么涨价,其市场价格就在某个高点附近陷入短暂的均衡3。
- 泡泡玛特火的很莫名其妙,因此,如果泡泡玛特再推出一个产品,销量可能爆也可能无人问津(网红产品属性)。
将炫耀性消费纳入模型
观点很简单,这里主要是看怎么纳入经济学理论模型。
于此同时,在 1991 年的芝加哥大学经济学课堂上,诺奖得主 Gary S. Becker4提出一个问题——为什么他喜欢的一家著名的海鲜餐厅每天来客这么多,却从来不提高价格?
这类现象非常广泛——在没有黄牛的时间里,许多成功的餐馆、戏剧、体育赛事和其他活动即使在持续的过度需求下也不会提高价格。
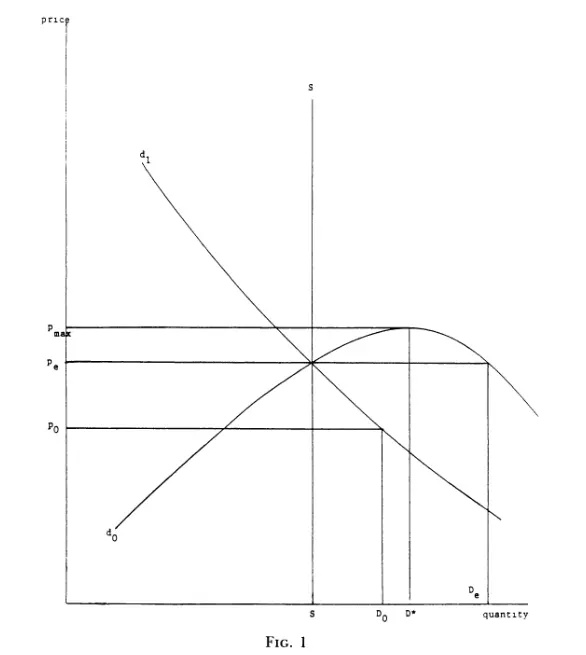
传统微观模型
在这个价格-需求图中,$d_0$ 为生产函数5,$d_1$ 为需求函数。$s$ 为热门餐厅的座位数量。目前热门餐厅情况是需求大于供给,对应的价格水平为 $p_0$。显然,当价格提升到 $p_e$ 时,餐厅能赚更多。价格提升到 $p_{max}$,利润则取决于双方的弹性。
$$ \pi(P)=P\cdot Q(P)-C(Q(P)) $$ $$ \frac{d\pi}{dP}=Q(P)+P\cdot\frac{dQ}{dP}-C^{\prime}(Q)\cdot\frac{dQ}{dP} $$ $C^{\prime}(Q)$ 可以写成边际成本 $MC$,同时定义价格需求弹性 $\varepsilon\equiv\frac{dQ}{dP}\cdot\frac{P}{Q}$。
$$ \begin{aligned}\frac{d\pi}{dP}&=Q+P\cdot\left(\varepsilon\frac{Q}{P}\right)-MC\cdot\left(\varepsilon\frac{Q}{P}\right)\\&=Q+\varepsilon Q-\varepsilon Q\cdot\frac{MC}{P}\\&=Q\left(1+\varepsilon-\varepsilon\frac{MC}{P}\right).\end{aligned} $$ 一阶条件就是著名的:
$$\frac{P-MC}{P}=-\frac{1}{\varepsilon}$$ 消费弹性和厂商加价的空间密切相关。当我们考察厂商市场势力时,可以尝试从这个式子出发进行估计。
炫耀消费的模型
消费者在购买商品时,会考虑这个商品的市场。例如后续发小红书、朋友圈和群体“同屏共振”的价值。此时需求函数变为:
$$ D=\sum d^{\prime}(p,D)=F(p,D),\quad F_p<0,F_d>0 $$
- 套娃一下——市场总需求 D 由每个人的需求 d 加总而成,而每个人的需求函数会考虑市场总需求 D。
- 市场总需求函数依旧价格越高需求越少($F_p<0$)。
- 市场也会有正反馈的结构,买的人越多,被吸引过来的人也会越多($F_D>0$)(网络效应)。
接下来对总需求函数求微分方程:
$$L(p,D)=F(p,D)-D=0$$ $$ dL=L_pdp+L_DdD=0 $$ 此时,
$$ L_p=F_p,\quad L_D=F_D-1 $$
最终得到,
$$ F_pdp+(F_D-1)dD=0 $$
变形,就会得到价格对需求的变化率6:
$$ \frac{dp}{dD}=G_D=\frac{1-F_D}{F_p} $$ 这里的 $G_d$ 表示逆需求函数对需求 d 求导。
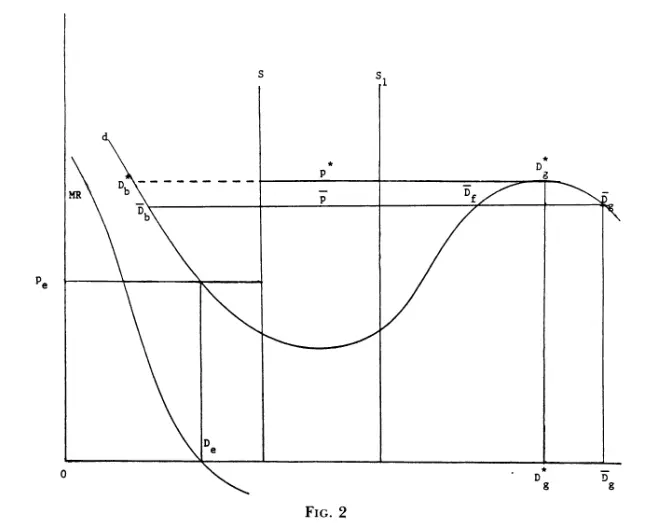
如果社会效应足够强—— $F_D>1$ —— $\frac{1-F_D}{F_p}>0$。从变化率上看——价格会随着需求增多而增多。直到厂商进入生产的第三阶段拐点 $p_{max}$(兼容了传统解释,就是图 3 的内容)。
但是现在基于网络模型有了一种新的可能——
在总需求较少时,$F_D<1$; 在总需求较多时,$F_D>1$。
此时,社会总需求函数不再是单调下滑的线,而是先下降再上升的曲线。
假设固定成本,
$$ \begin{aligned} MR&=\frac{d(PD-C)}{dD}\\ &=P+D\frac{dP}{dD}\\ &=P+D(\frac{1-F_D}{F_p}) \end{aligned} $$ 由于需求较少阶段 $\frac{dp}{dD}=G_D=\frac{1-F_D}{F_p}<0$,此时就是斜率向下的曲线。
实际上,MR 曲线和 D(P) 需求曲线的高低和倾斜程度可以如此比较:
高度(基于 MR 的式子就可以看出): $$ MR-D(P)=D(\frac{1-F_D}{F_p}) $$ 因此,开始阶段 MR 曲线在需求曲线下方。
此时就是现实中的多重均衡!例如定价在 $p^*$。
- 如果产品一炮而红,口碑出圈,那么市场需求就会叠加到 $D_g^*$ 水平。
- 如果产品其实无人问津,实际的需求就在 $D_b^*$ 水平。
在这种不确定性,厂商一般更加厌恶生产过剩($s-D_b^*$)。因此厂商会倾向于选择 $MR=0$ 的均衡水平。
模型的意义
- 这个模型解释现实商店经验为什么广告和营销如此重要(这点很自然)。
- 其中最不容易想到的是——为什么网红厂商在热销期间会维持一种保守定价。本质还是网络效应带来的不确定性。
- 模型也较为优雅的刻画了进入热门阶段的均衡为何如此短暂——此时价格函数变动的空间并不大——当网络效应持续变弱,价格也会自动走低。
- 目前来看,网络效应的变量刻画还有值得探索的空间。
退一步来理解网络效应
个体的效用为
$$ U_i=U(x_i,y_i;X) $$
其中,$X=\sum x_{j}$ 表示网络效应。
接下来求解边际条件:
$$ MU_{x_i}=\frac{\partial U}{\partial x_i}+\frac{\partial U}{\partial X}\cdot\frac{\partial X}{\partial x_i} $$ 如果 $\frac{\partial U}{\partial X}$ 很大,意味着一种外部性,消费者购买网红产品时,其额外带来了社交属性的满足,甚至可能超过了价格上升带来的负效用。
从网络效应到复杂经济学
网络效应其实就类似一种多重结构的正反馈和负反馈。
大道向来不会用狭小的概念。
区域经济学,空间自相关也是种网络效应。区域经济学的距离方位一直都不“狭义”——文化距离(例如方言区)、经济距离(产业结构)、认知距离(例如产业结构竞争或者互补、专利相似度)………
就如同凯恩斯理论中的乘数效应。其实凯恩斯还有多重均衡的概念。一个经济体,在某些条件下可能存在多重均衡。
由于利率、价格、工资调整不完全,社会有一种自发的强化效应。。人们的情绪在乐观和悲观中交替且互相传染,这就是凯恩斯所说的"动物精神"。正因如此,社会预期的调整、经济信号的秩序规范才如此重要。
这也是为什么凯恩斯7如此说到
“在短期内,人们的心理预期和信心(animal spirits)比黄金储备更重要。”
经济学到今天,已经迈向了复杂经济学。复杂经济学家们重视社会中的网络效应、异质性主体、多重均衡。其实网络效应的解释也很简单,我跟随着社会的声音起伏,只是如何提取社会的声音并纳入分析?这就是最值得探索的议题之一。