生命周期与工资分解

起因是看到了《中国工业经济》的《户籍制度下劳动力的经验人力资本: 生命周期视角》 ¹，觉得关于生命周期工资的分解理论太顶级了，这样的思路怎能不发顶刊！？在阅读过程中发现其分析框架果然来自 JPE 的《Life cycle wage growth across countries》（2018）²的 Heckman-Lochner-Taber 算法（简称 HLT），沿用的也是里面的 do 文件，这里记录下学习 HLT 的笔记，并且记录理论变化和数理推导过程。

在查找相关文献中也发现了很多基于 HLT 法本土化的论文——如何把国外优秀论文化为己用，怎么找到微小的计量创新点，看看别人做了哪些微改变确实让人深思，这点在最后分享（dog.jpg)

APC 面板与生命周期

明瑟收入方程（Mincer earnings function) 较早讨论了人力资本投入的回报关系³：

$$ ln(w)=\alpha_0+\beta_ss+\beta_0\exp+\beta_1\exp^2+\gamma X_i+\varepsilon$$

$s$ 代表受教育水平，$exp$ 代表工作经验水平 $experience$ ， $X_i$ 是其他控制变量。

这里假设了对于对数化后的工资来说，教育回报是线性的，工作经验回报是非线性的。Heckman 等人（2006）相关研究中通过实证检验这个假设是对的 ⁴。

就算不讨论方程形式，这样的分解变量肯定是不够的。

著名面包猎人 DIO 曾说过“JOJO，我在短暂的人生里发现… 一个人越是玩弄阴谋，就越会感到人类的能力是有极限的….”没错! 人类的寿命和身体阶段是我们不得不关注的点！一旦我们谈及劳动经济学，就离不开谈论人的年龄和状态。

首先我们考虑生命周期——不同年龄的人就算有同样的学历和工作经验甚至更高，教育回报率也不同，这里估计参数年龄和时间相关。同时，每个人所处的时代背景也会对工资收益造成影响，例如上山下乡、改革开放都深入地影响了那一批人，这里估计参数（一般通过出生年份标记分类）个体队列分组也和时间相关。时间效应（包括经济周期和线性增长，例如工资通货膨胀）还是和时间相关！以上参数通通和时间相关！在计量方程中如何分解就成了大难题。于是就有了如下扩展的灵活的明瑟方程。

$$ln(w_{ict})=\alpha+\theta(s_{ict})+f(x_{ict})+\gamma_{t}+\chi_{c}+\varepsilon_{ict}$$

$i$ 代表个体编号。 $c$ 代表分组编号，例如改革开放时出生的是一组，上山下乡时出生的是一组，也就是队列分组 ⁵。在生命周期中，一般以五年工作经验为一组进行切片。下图的描述统计就是通过五年分组后组与组比较展现的生命周期初步描述统计。$t$ 代表时间变量。$\theta(s_{ict})$ 代表教育收入函数，$f(x_{ict})$ 代表工作经验收入函数，$\gamma_t$ 代表分组 $c$ 的队列效应， $\chi_t$ 代表分组队列效应，$\varepsilon_{ict}$ 为误差。

个体追踪的面板数据很难直接获得。于是 Deaton 提出：

我们不要个体追踪面板了！这个家里已经没有你得到位置了！我们用人口普查的一次次截面合成出“伪面板” 流行病理学，药物试验，社会心理等统计领域都会运用这种伪面板。

例如下图：这类收入比较数据不是个体追踪面板数据，而是由同一时间不同年龄的截面数据构造出的伪面板。

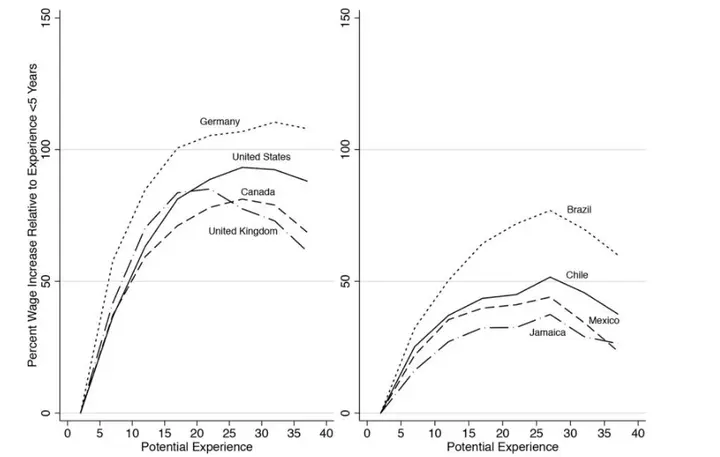
这种面板数据要考虑年龄 age、时间段 period、群组 cohort作为自变量，也叫 The Age-Period-Cohort Model（简称 APC）。在劳经中，APC 面板数据的估计一直是个热点⁶ (大神 Deaton 力挺，毕竟是自己在经济分析中建立的框架）。

对于估计式：

$$ln(w_{ict})=\alpha+\theta(s_{ict})+f(x_{ict})+\gamma_{t}+\chi_{c}+\varepsilon_{ict}$$

当我们使用 APC 数据直接回归时，会产生共线性的问题——年龄+出生年份=当前年份。

Deaton 的方法（数理分解）

Deaton 全名Angus Deaton，2015 年因为贫困研究获得诺贝尔奖，其最多的贡献其实是劳动经济学，被人热议的成果是援助可能使处境更坏 ⁷。

下面方法主要参考了他的著作《The analysis of household surveys: A microeconometric approach to development policy》（1997）（第 123 页开始），说实话，感觉写的，，不太友好。

对于公式：

$$ln(w_{ict})=\alpha+\theta(s_{ict})+f(x_{ict})+\gamma_{t}+\chi_{c}+\varepsilon_{ict}$$

也就是

$$w_{ict}=\exp (\alpha+\theta(s_{ict})+f(x_{ict})+\gamma_{t}+\chi_{c}+\varepsilon_{ict})$$

加总后的总工资可以分解为先按照 $c$ 进行分组加总，每组里按照个体 $i$ 加总：

$$\begin{aligned} \sum_{i=1}^{N_{ct}}w_{ict}=& \sum_{i=1}^{N_{ct}}\exp(\alpha+\theta(s_{ict})+f(x_{ict})+\gamma_{t}+\chi_{c}+\varepsilon_{ict}) \newline &=\exp(\alpha+\gamma_t+\chi_c)\underbrace{\sum_{i=1}^{N_{ct}}\exp(\theta(s_{ict})+f(x_{ict})+\varepsilon_{ict})}_{F_{ct}} \newline &=\exp(\alpha+\gamma_{t}+\chi_{c})F_{ct} \end{aligned}$$

$F_{ct}$ 此时就是受教育经验函数 $\theta(s_{ict})$ 和工作经验函数 $f(x_{ict})$ 工资贡献总和。

定义 $\bar{F}_t=\sum_{c\in C_t}F_{ct}$，接下来继续把这部分分离出去，变形如下：

$$\begin{aligned} W_{t}=& \sum_{c\in C_{t}}\sum_{i=1}^{N_{ct}}w_{ict} \newline &=\sum_{c\in C_{t}}\exp(\alpha+\gamma_{t}+\chi_{c})F_{ct} \newline &=\exp(\alpha)\exp(\gamma_{t})\sum_{c\in C_{t}}\exp(\chi_{c})F_{ct} \newline &=\exp(\alpha)\exp(\gamma_{t})\bar{F}_{t}\sum_{c\in C_{t}}\exp(\chi_{c})\frac{F_{ct}}{\bar{F}_{t}} \end{aligned}$$

此时，工资就可以分解三部分：时间效应 $\Gamma_{t}$、工作经验和教育效应 $\bar F_{t}$、队列效应 $\bar X_{t}$。

$$W_{t}=\underbrace{\exp(\gamma_{t})}_{\Gamma_{t}}\bar F_{t}\underbrace{\sum_{c\in C_{t}}\exp(\chi_{c})\frac{F_{ct}}{\overline{F_{t}}}}_{\tilde{X_{t}}}$$

工作经验和教育效应都可以通过受教育年份、工作年份量化参数，但是时间效应和队列效应很难被识别，因此这样处理的目的就是单独提炼出时间、队列效应进行研究，于是定义：

$$\Omega_{t}=\frac{W_t}{\bar F_{t}}=\Gamma_{t}\bar{X}_{t}$$

在研究队列效应和时间效应，我们一般从两种角度进行分解。

• 时间趋势：我们的科技总是向前的，这种随着时间平均进步的就是时间趋势。

• 周期性: 例如时令蔬菜，供给需求循环周期，例如婴儿潮——婴儿潮出生的那一代在中年期时也会出现劳动力高峰。

  

此时再次对数化—— $\omega_t=\log\Omega_t,\bar{\chi}_t=\log\bar{X}_t，\bar{\gamma}_t=\log\bar{\Gamma}_t$

同时要强调定义的是此时 $\bar{\chi}_t$、 $\bar{\gamma}_t$ 是样本均值的偏差。就像我们假设回归后的残差和为 0 一样，这个假设同样要求样本均值残差和为 0：

$$\frac1T\sum_{t=0}^T\gamma_t=\frac1T\sum_{t=0}^T\bar{\chi}_t=0$$

此时式子分解为：$\omega_t=\bar{\omega}+\bar \gamma_t+\bar{\chi}_t$

原论文中只交代了 $\bar{\omega}$ 是“an appropriately chosen constant”。个人认为它就是样本均值，于是相对的，$\bar{\chi}_t$ 、${\bar \gamma}_t$ 就是样本均值的偏差。

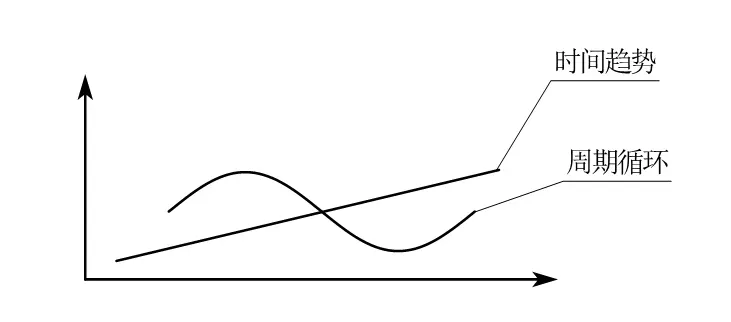
此时时间效应、队列效应都可以分解成时间趋势$g$ 和周期性变动 $u$ ,可使用 $gt+u$ 表示，得到如下分解：

$$\gamma_{t}=g_{\gamma}t+u_{\gamma,t},\quad\bar{\chi}_{t}=g_{\bar \chi}t+u_{\bar \chi,t}$$

我们使得 $g_{\omega}=g_{\bar \gamma}+g_{\bar{\chi}}$，最终估计就变成了 $$\omega_t=\bar{w}_t+g_\omega t+u_{\omega,t}$$

Deaton（1997） ⁸处理到这里就无能为力了，他只能进行枚举法处理。

• 残差分解全部解释为时间效应： $g_{\omega}=g_{\bar \gamma}+g_{\bar{\chi}}=g_{\bar \gamma}$
• 残差分解全部解释为队列效应： $g_{\omega}=g_{\bar \gamma}+g_{\bar{\chi}}=g_{\bar{\chi}}$
• 你俩五五开，各分得一半： $\frac{1}{2}g_{\omega}=g_{\bar \gamma}=g_{\bar{\chi}}$

计量分解

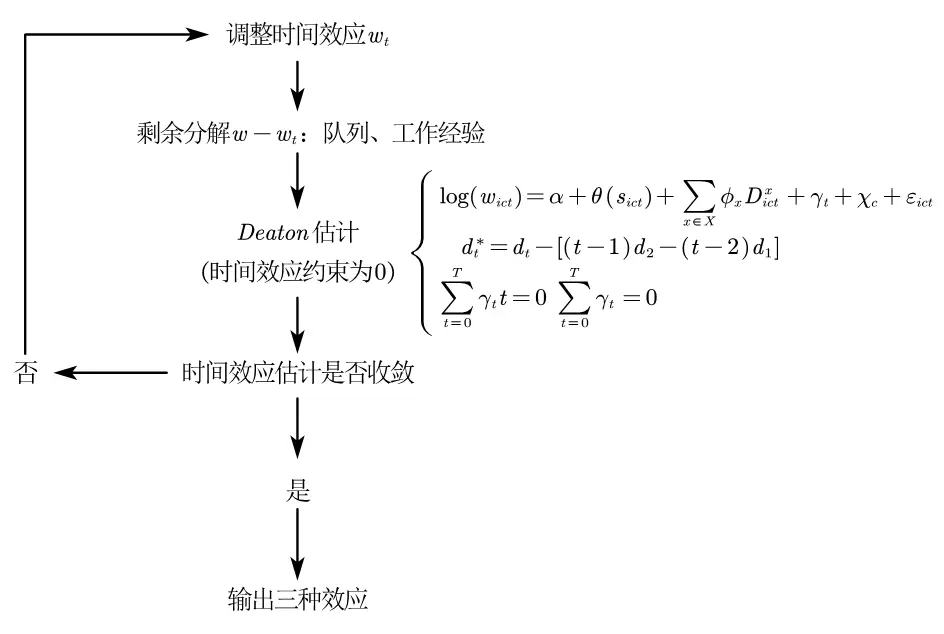
也就是估计以下式子：

$$\log(w_{ict})=\alpha+\theta(s_{ict})+\sum_{x\in\mathbf{X}}\phi_{x}D_{ict}^{x}+\gamma_{t}+\chi_{c}+\varepsilon_{ict}$$

$\theta(s_{ict})$ 表示受教育年龄的收入函数，一般线性表示。

$D_{ict}^{x}$ 为生命周期每个年龄段的虚拟变量。

$\gamma_{t}$: 时间效应。$\chi_{c}$ 个体效应。

直接用这个式子回归，$D_{ict}^{x}$、$\gamma_{t}$、$\chi_{c}$ 具有共线性，Deaton 法方法是给 $\gamma_{t}$、$\chi_{c}$ 额外施加一个线性约束。当我们设置只有队列效应，时间效应为 0 时，需要满足 $\sum_{t=0}^{T}\gamma_{t}t=0$。我们可以通过“标准化” $\gamma_{t}$ 实现这一点：

定义

$$\quad d_t^*=d_t-[(t-1)d_2-(t-2)d_1]$$

$t$ 是年份标号，当这条数据是 $t$ 年时，则为 1，否则为 0。对应 stata 操作就是

1

tab year ,gen(d)

举例如下，

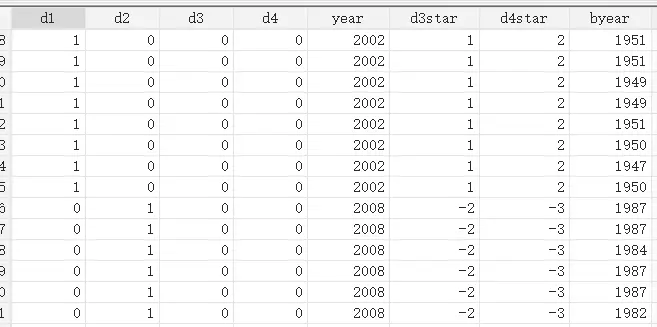
高阶差分法估计

Deaton 估计年份、队列效应其实是有一点极端了，要么通吃，要么平分，被后来人批判“没有理论基础”。有学者提出，我们求不了增长率（一阶导数），那我们就利用高阶差分估计二阶及其以上的，这样就可以验证年份、群组效应的大致形状了！

想看超细节推导建议查看《Disentangling age, cohort and time effects in the additive model》（McKenzie 等，2006）⁹。

对于估计式： $$ ln(w_{ict})=\alpha+\theta(s_{ict})+f(x_{ict})+\gamma_{t}+\chi_{c}+\varepsilon_{ict} $$ 直接回归会有共线性的问题——年龄+出生年份=当前年份。我们无法直接估计 $\gamma_t$、$\chi_t$ 的形式（例如凹凸性），但我们可以通过差分法，研究分组相减后的高阶差分的性质，进而往低阶差分估计。

此处生命周期模型中，教育年份是线性估计且容易分解，我们先忽略掉¹⁰。个体编号为 $i$ ,按照生命周期进行队列分组 $c$ ， $k$ 是工作经验，等于 $t-c$。每组队列对应方程如下： $$ y_{ct}=\alpha+\beta _kx_{ct}+\gamma_{t}+\chi_{c}+\varepsilon_{ct} $$

强调！也就说 $\beta_{\color{red}{k}}$ 的 $\color{red}{k}$ 的估计与 $\color{blue}{k=t-c}$ 密切相关！！！！我们正是利用这一点进行高阶差分估计。

我们在同一组内（例如选择中年那一组 $c_1$ ），使用 $y_{c_1,t_2}$ 的数据减去 $y_{c_1,t_1}$ 进行组内时间上的一阶差分：

生命周期中，每组队列时间差均匀分布，基本五年一组，也就是 $$ (x_{ci,t+1}-x_{ci,t})=(x_{cj,t+1}-x_{cj,t})=\Delta x_t $$ 于是式子可以进行以下变形： $$ \begin{align} &y_{c_1,t_2}-y_{c_1,t_1}\newline &=(\beta_{\color{red}{k_{2}}}- \beta_{\color{red}{k_{1}}})(x_{c_1,t_2}- x_{c_1,t_1})+(\gamma_{t_2}-\gamma_{t_1})+(\varepsilon_{c_1,t_2}-\varepsilon_{c_1,t_1})\newline &=(\beta_{\color{red}{k_{2}}}- \beta_{\color{red}{k_{1}}})\Delta x_t+(\gamma_{t_2}-\gamma_{t_1})+(\varepsilon_{c_1,t_2}-\varepsilon_{c_1,t_1})\newline \end{align} $$ 对应的时间关系 $k=t-c$，我们再对另一个同一组内进行时间上的一阶差分。

我们选择相对 $c_{1}$ 组更年轻的一组 $c_{0}$（视为青年组）, 得到 $k_2=t_1-c_0,k_3=t_2-c_0$。

此时得出一阶差分： $$ \begin{align} &y_{c_0,t_2}-y_{c_0,t_1}\newline &=(\beta_{\color{red}{k_{3}}}- \beta_{\color{red}{k_{2}}})\Delta x_t+(\gamma_{t_1+1}-\gamma_{t_1})+(\varepsilon_{c_0,t_2}-\varepsilon_{c_0,t_1})\newline \end{align} $$ 此时，我们把 $c_1$ 和 $c_0$ 两组时间一阶差分再相减： $$ \begin{align} &[y_{c_1,t_2}-y_{c_1,t_1}]-[y_{c_0,t_2}-y_{c_0,t_1}]\newline &=(\beta_{\color{red}{k_{2}}}- \beta_{\color{red}{k_{1}}})\Delta x_t+(\gamma_{t_1+1}-\gamma_{t_1})+(\varepsilon_{c_1,t_2}-\varepsilon_{c_1,t_1})\newline &-(\beta_{\color{red}{k_{3}}}- \beta_{\color{red}{k_{2}}})\Delta x_t-(\gamma_{t_1+1}-\gamma_{t_1})-(\varepsilon_{c_0,t_2}-\varepsilon_{c_0,t_1})\newline &=[(\beta_{\color{red}{k_{2}}}- \beta_{\color{red}{k_{1}}})-(\beta_{\color{red}{k_{3}}}- \beta_{\color{red}{k_{2}}})]\Delta x_t-\Delta_{c}\Delta_{t}\varepsilon_{c_{0},t_{2}} \end{align} $$ 我们可以发现，此时这个高阶差分不含有时间效应 $\gamma_t$ 和队列效应 $\chi_c$。

$[(\beta_{\color{red}{k_{j}}}- \beta_{\color{red}{k_{j-1}}})-(\beta_{\color{red}{k_{j+2}}}- \beta_{\color{red}{k_{j}}})]$ 也具有几何含义。对于式子： $$ y_{ct}=\alpha+\beta _kx_{ct}+\gamma_{t}+\chi_{c}+\varepsilon_{ct} $$ $[(\beta_{\color{red}{k_{j}}}- \beta_{\color{red}{k_{j-1}}})-(\beta_{\color{red}{k_{j+2}}}- \beta_{\color{red}{k_{j}}})]$ 是 $\beta _k$ 的斜率。类似于我们无法看出函数一阶导的情况，但是我们搞导了二阶导的情况，二阶导能告诉我们的，正是函数的凹凸性和增长率的边际作用。于是对于每一组 $c$ ,我们都有了它二阶斜率的估计量。

同样的方法，我们估计三种效应的高阶差分如下：

以下是个人配平的，就是利 $k=t-c$ 消掉参数。

$$ \begin{cases} \text{age effect} \newline :[y_{c_i,t_{i+1}}-y_{c_i,t_i}]-[y_{c_{i-1},t_{i+1}}-y_{c_{i-1},t_i}]\newline \text{time effect}\newline :[y_{c_i,t_{i}}-y_{c_{i},t_{i-1}}]-[y_{c_{i+1},t_{i+1}}-y_{c_{i+1},t_{i} }]\newline\text{chort effect} \newline :[y_{c_i,t_{i}}-y_{c_{i-1},t_i}]-[y_{c_{i+1},t_{i+1}}-y_{c_{i},t_{i+1} }]\newline \end{cases} \newline $$

HLT 法

全名 heckman-lochner-taber。这里的介绍重点参考《“golden ages”: A tale of the labor markets in China and the united states》（Hanming 等，2023）的附录部分¹¹ 。原文见《Life cycle wage growth across countries》（Lagakos 等，2018）

前文的方程估计把工资贡献分解为：工作经验、队列、年龄、教育。

这是导致共线性的原因，这种分解却并非永久存在的。

如果从生命周期视角审视人的工资增长，可以提出一个假设：一个人在即将退休时，他会放弃任何人力资本投入，这时候他的工资增长来源只有时间效应。 此时在两个队列中，同样的 $t$ 年份时间段内，老年组工资增长率为 1%；青年组增长率为 5%，那么说明 1%是时间效应贡献的，4%是队列效应+工作经验¹² 。那么可以通过不断调整收入效应来研究各组别老年时时间效应是否趋于一致。

此时，折旧率 $\delta$ 可用来进行敏感度测试。

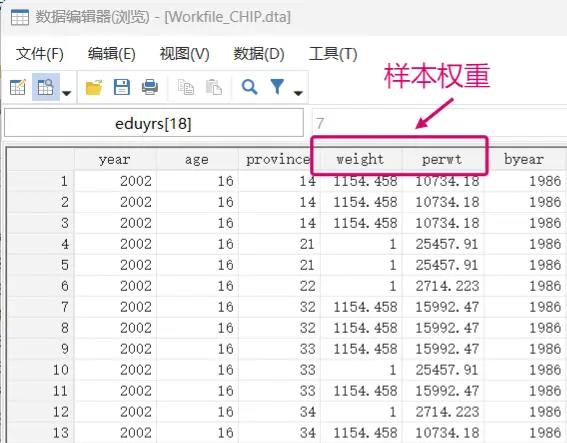
该算法文件可以反复使用，只是 do 文件中的一个变量“perwt”让人在意，参考解释为“individual weights”。我看到的所有文章都没有交代怎么生成的样本权重变量。参考美国 INPUMS 统计局的解释是“一个样本代表了总体多少人”。也可以参考下面这篇文章了解样本权重的重要性和生成方式:

如何对抽样调查数据进行加权？ ——关于CHIP数据权重的建议

批发的创新

首先感叹 top 5 的期刊就是不一样，在经济意义、计量识别上都做到了创新。Deaton 大神在学术创新上既开创了 APC 伪面板的诸多估计方法，又扩展了经济家庭分析的理论面。从明瑟方程到借助生命周期理论处理 apc 面板的内生性，理论创新，算法创新这些是 top 5 干的事。 $$ \text{minser function}\rightarrow \text{APC model} \rightarrow \text{APC+life cycle} $$ 接下来往下，确实就是批发微创新了——

• 数据创新：用完全一样的框架分析不同数据，例如智利的一篇《Returns to work experience in chile》，使用智利本土数据重新跑了一下。中国人口数据库一直是不缺的，例如 CFPS、CGSS、CHIP、CMDS……
• 本土变量创新： 原算法比较的是国家之间，《户籍制度下劳动力的经验人力资本: 生命周期视角》换成了外来劳动力和流动劳力, 结合我国的义务教育法也重新估算了“潜在工作经验”。如果去多多检索，还有换成工农业、高中生大学大专教育分类、性别分类的文章。
• 缝合创新： 还是以《户籍制度下劳动力的经验人力资本: 生命周期视角》为例子：缝合了生命周期的测量和人力资本的测量，把两个框架缝合。
• 分析变量创新 ：个人觉得《golden ages: A Tale of the Labor Markets in China and the United States》的创新让人印象深刻——利用算法没有挖掘的其他因素。HLT 原文比较了生命周期曲线的陡峭，而作者另辟曲径，比较了生命周期的顶点变动，把其称为“golden ages”。别人比较了曲线，我就比较拐点，别人比较了空间差异，我就再多关注时间差异，并且取名为“中美黄金年龄的演变”。旧瓶新酒，亦有新芳——讲故事的能力实在让人拍案叫绝。