计量数据的分组与测度（STATA 版）

2023-12-26 约 10272 字预计阅读 21 分钟次阅读

很多时候，我们总强调数据量的庞大，认为数据越多就越有代表性，从而忽视了数据结构的分析，进而导致了错误的估计。不恰当的估计方法会带来与现实完全相反的结果。为更好地了解数据结构，经济学有了固定效应、调节效应、异质性分析、稳健性分析。这些看起来是实证范式截然不同的部分，但个人理解他们都是为了区分数据结构进行分类，以保证我们的结论是真正有效的。因此，本文想从数据结构与变量分类的角度重新理一下实证论文的操作意义，并且区分 stata 不同的回归命令。

下面以范里安《微观经济学：现代观点》的第 17 章“测度”中的一个例子引入。

一、统计学的悖论

辛普森悖论

假设我们想要研究“咖啡消费与收入”的关系。有这样一组数据，4 位男性和 4 位女性，以及他们的收入和咖啡消费情况。

Stata 数据生成如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


clear
input str6 gender income coffee
"woman" 8 1
"woman" 9 2
"woman" 10 3
"woman" 11 4
"man" 1 6
"man" 2 7
"man" 3 8
"man" 4 9
end

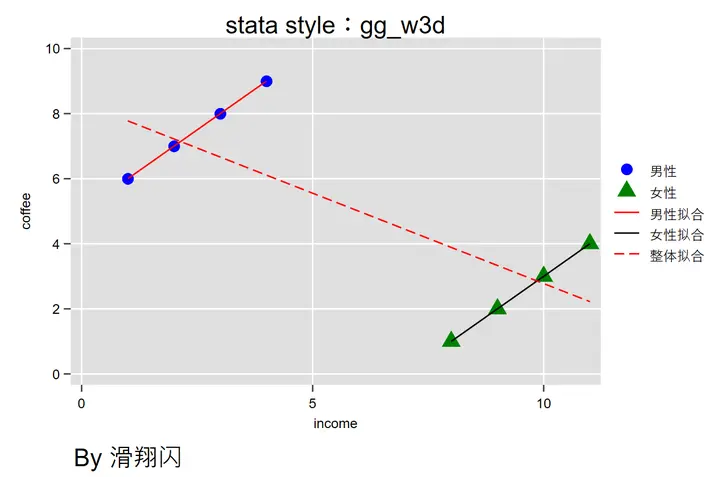
然后我们可以画出散点图进行三次不同样本数的拟合，分别是整体一次，男性一次，女性一次：

/img/计量数据的分组与测度（STATA版）.zh-cn-20240523103053504.webp — 用这个风格画stata基本能做到和R语言效果类似——绘图代码放在下面：

用这个风格画 stata 基本能做到和 R 语言效果类似——绘图代码放在下面：

1
2
3
4
5
6
7
8
9


*ssc install schemepack, replace  //绘画风格命令
*介绍详见：https://www.lianxh.cn/news/e76a8a7e3c6c4.html
  set scheme gg_w3d
  
twoway scatter coffee income if gender == "man",color(blue) msize(3) || scatter coffee income if gender == "woman",color(green) msize(3) msymbol(triangle) || lfit coffee income if gender == "man",color(red) || lfit coffee income if gender == "woman" ,color(black) || lfit coffee income ,color(red)  lpattern(dash) ///
		legend(order(1 "男性" 2 "女性" 3 "男性拟合"  4 "女性拟合"  5 "整体拟合" )) ///
		xtitle("income") ytitle("coffee") ///
		title(stata style：gg_w3d) ///
		note("By 滑翔闪")

如果我们不管三七二十一，直接对总体数据进行回归拟合，我们会得出来 收入越多，咖啡消费越低 的结论，但如果我们分别对男性和女性进行回归拟合，得到的结论却完全相反——“收入越多，咖啡消费越多”。显然，后者更贴合现实情况。

这就是 $\boxed{辛普森悖论}$：局部的相关性和整体的相关性可能呈现截然不同的结果。

辛普森悖论在生活中比比皆是，例如各个年龄段的人服用药物后的疗效测量、各个学院录取学生是否有性别歧视、警察执法是否有种族歧视……

我们不但要关心数据的绝对值，例如某个结果的性别比；
还有观察相对数值，例如警察执法更关注有色人种，那么前提是有色人种是不是犯罪率更高些；

《An alternative test of racial prejudice in motor vehicle searches: Theory and evidence》（2006）¹中就是基于“不同人种犯罪率与警察执法关注度”来研究佛罗里达的警察执法是否涉及种族歧视。自从佛洛依德（Floyd）的“I can’t breathe”出圈后，很多书都热衷于通过这个事件引出真正的反事实推断²（例如《基本无害的计量经济学》（Joshua D. Angrist））

还要注意内部的分层讨论，分种族、分地域、分性别……也就是上面这个喝咖啡的例子。

导致辛普森悖论的其中一个原因就是遗漏变量和混杂因子³——在咖啡消费与收入中，性别是一个重要影响因素，我们遗漏了，但是通过分组拟合实现了控制。

其他类似的悖论还有幸存者偏差、柏克森悖论…… 两者是无意识地筛选了样本从而影响了分析结果。

二、面板数据

截面数据同一时间/对象不同空间、时间序列同一空间/对象不同时间、面板数据不同时间不同空间/对象。
面板数据天然的多了两个值得讨论的变量——空间/对象和时间。

经济学常使用面板数据分析现实。

$$ 数据\begin{cases} 一维\begin{cases}时间序列：时间\newline 截面数据：空间 \end{cases}\newline 二维(面板数据)：时间+空间\newline 高维：更多维度 \end{cases}\newline $$ $$ 面板数据\begin{cases} 平衡/非平衡（时间空间数之比是否一致）\newline 长/短（空间数是否少于时间数） \end{cases}\newline $$

对于数据面板，我们首先要明确哪个维度对应了时间、哪个维度对应了空间/对象。其实就是一个分组的过程，你可以从行业的角度分组，也可以每个人单独编号 id 分组。用 stata 的语言来说，就是：

1

xtset id year

三、残差经济、数学、统计含义

普通的回归方程OLS是： $$ Y=\alpha X +u $$ 直接对数据整体进行拟合。当我们知道辛普森悖论后，我们知道这样做回归是整体拟合，可能与局部拟合是完全不一样的结果。残差$ \color{red}{u} $遗漏的我们没关注的信息太多了，例如性别分类。所以我们要进行分组，把性别变量 M 从残差 $\color{red}{u}$ 中分解出来。

$$ Y=\alpha X +\beta M+u $$ 其实这时候就有了 $\boxed{控制变量}$。注意！这里是我个人从分组的视角引出控制变量，是强调控制变量在选择性偏差的作用，这种分组需要充分考虑控制变量对我们研究的实际经济意义，例如大量研究表明不同性别的咖啡消费习惯确实不同。控制变量的选择的其他重要作用是减少混杂因子干扰；此外，我们还要考虑最优拟合、无偏估计等统计学上的数学意义。

有了面板数据后，我们的式子变成了二维，有了对象\空间的编码 i 和时间的编码 t 。普通的回归方程 OLS 变为： $$ Y_{\color{red}{it}}=\alpha X_{_{\color{red}{it}}}+\beta M_{_{\color{red}{it}}}+u_{_{\color{red}{it}}} $$ 为了进一步分解时间和空间/对象两个维度的残差的经济解释，我们又继续分解 $$ Y_{\color{red}{it}}=\alpha X _{_{\color{red}{it}}}+\beta M_{_{\color{red}{it}}}+\lambda_{\color{red}{i}}+\gamma_{\color{red}{t}}+u^{\prime } $$ 于是式子就变成了这样：

$$ Y_{\color{red}{it}}=\alpha X _{_{\color{red}{it}}}+\beta M_{_{\color{red}{it}}}+\lambda_{\color{red}{i}}+\gamma_{\color{red}{t}}+u^{\prime } $$ 首先我们来分析他们的经济意义——变量：

$\boxed{\gamma_{\color{red}{t}}}:$ 这部分残差是时间维度的分解，说明这部分变动只和时间相关，是时间效应，例如时令蔬菜产量显然和季节相关，长期来看技术自然而然的稳定进步。同时这些效应是每个个体共享的，也就是所有样本都在随时间同步改变的变量。

$\boxed{\lambda_{\color{red}{i}}}:$ 这部分残差是空间/对象维度的分解，说明这部分变动只和个体相关，是个体效应，例如苹果公司就是拖了很久才出 C 口，这就是他们的企业文化，只有苹果有这种想法，而且相当长的时间里，同类企业里只有他们坚持这么干。

$\boxed{u_{\color{red}{it}}^{\prime }}:$ 现实值和估计值的偏差，在我们的模型解释之外, 是残差。导致的原因有很多，例如测量误差、遗漏变量、模型不符合现实……

然后我们来分析他们的数学意义——截距：

$$ Y_{\color{red}{it}}=\alpha X_{_{\color{red}{it}}}+\beta D_{_{\color{red}{it}}}+(\lambda_{\color{red}{i}}+\gamma_{\color{red}{t}}+u^{\prime }) $$ 显然，$(\lambda_{\color{red}{i}}+\gamma_{\color{red}{t}}+u^{\prime })$ 作为常数，在线性方程的结构中就是截距！

最后我们来分析他们的统计学意义——残差：

是否有不同的截距，这与残差的分布情况、异方差、相关性等方面密切相关。固定效应、随机效应、混合回归的一个区别是对残差的分解，我们认为我们的模型是否能解释个体效应、时间效应。

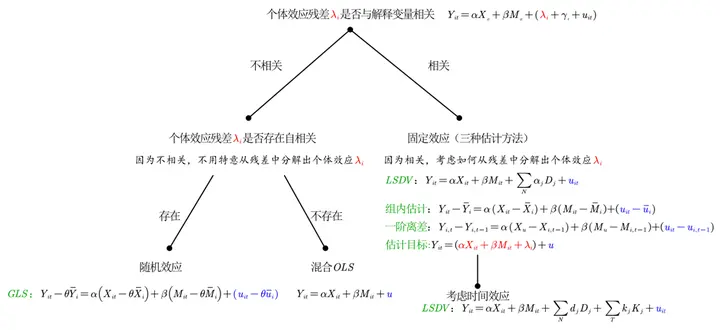
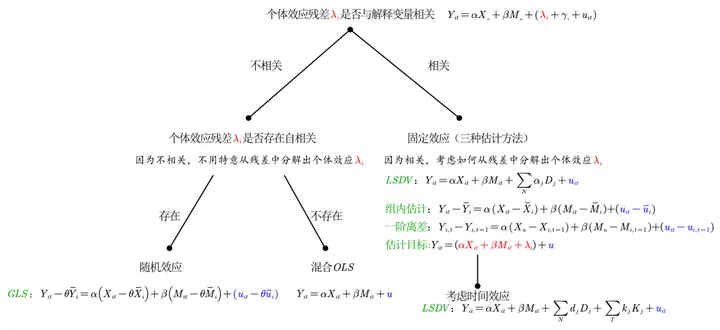
$$ Y_{\color{red}{it}}=\alpha X _{_{\color{red}{it}}}+\beta M_{_{\color{red}{it}}}+(\lambda_{\color{red}{i}}+\gamma_{\color{red}{t}}+u^{\prime }) \newline \xrightarrow{分解} 可解释部分+\color{blue}{不可解释部分}(误差) $$ 先放总结图，接下来展开解释

随机效应假设更加严格，也就是数据要求更高，因此大家才倾向于使用固定效应（也就是允许个体效应存在内生性）。

/img/计量数据的分组与测度（STATA版）.zh-cn-20240523103132982.webp — 先放总结图，接下来展开解释

通过经济意义、数学意义、统计意义的大致介绍，对于面板数据，我们有了不同的分解方法：

$$ Y_{\color{red}{it}}=\alpha X _{_{\color{red}{it}}}+\beta M_{_{\color{red}{it}}}+(\lambda_{\color{red}{i}}+\gamma_{\color{red}{t}}+u^{\prime }) $$

1、混合 OLS

$\boxed{混合OLS}$ : 当 $Y_{\color{red}{it}}=\alpha X _{_{\color{red}{it}}}+\beta M_{_{\color{red}{it}}}+(\lambda_{\color{red}{i}}+\gamma_{\color{red}{t}}+u^{\prime })=\alpha X _{_{\color{red}{it}}}+\beta M_{_{\color{red}{it}}}+u$ 时，也就是虽然我们有很多方法，比如可以按照年份分组、按照个体分组，但是还是把他们每个都看做独特的散点混合在一起进行回归，此时也就可以看做所有散点的拟合线共享一个截距。

此时假设个体效应不存在：$\lambda_{\color{red}{i}}=0$ 。

同时假设剩余残差与解释变量、控制变量都不相关：$Cov（u|M_{_{\color{red}{it}}},X_{_{\color{red}{it}}}） =0$，残差分布也满足正态分布。

$$ Y_{\color{red}{it}}=\alpha X _{_{\color{red}{it}}}+\beta M_{_{\color{red}{it}}}+u $$ 混合 OLS 就是用最小二乘法笼统地对所有点进行整体回归，所有散点的拟合线共享了一个截距 u⁴。因此混合 OLS 也叫“长截面回归”或者“合并截面回归”。

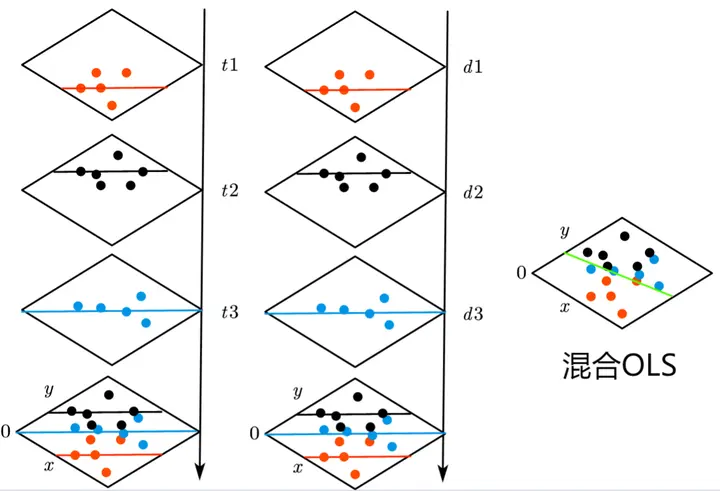
/img/计量数据的分组与测度（STATA版）.zh-cn-20240523103205584.webp — 第一列是按照年份分组，每个时间截面的散点拟合共享一个截距；第二列是按照个体分组，每个个体截面的散点拟合共享一个截距；第三列的图就是混合OLS，所有散点在一个面上直接进行拟合

第一列是按照年份分组，每个时间截面的散点拟合共享一个截距；第二列是按照个体分组，每个个体截面的散点拟合共享一个截距；第三列的图就是混合 OLS，所有散点在一个面上直接进行拟合

2、固定效应

分为个体固定效应和时间固定效应（双固定）。

个体固定效应：

$\boxed{LSDV} :$ 混合 OLS 是对所有$\lambda_{it}$一视同仁。想象一下，我们对同一个人观测多次，在混合 OLS 看来每次重复观测都有等同的价值。固定效应不这么认为，固定效应认为个体具有某种性质，重复观测获得的价值有限，所以我们需要生成虚拟个体变量（n-1 个）加入回归不对每类个体进行标识，单独估计每一个个体的效应，也就是“最小二乘变量模型（Least Square Dummy Variable Model）”（简称LSDV）。

会生成很多控制变量，所以 $R^2$ 很好。

$$ \begin{align} Y_{\color{red}{it}}&=\alpha X_{\color{red}{it}}+\beta M_{_{\color{red}{it}}}+\alpha_{1}D_{1}+\alpha_{2}D_{2}+\cdots+\alpha_{N}D_{N}+u_{\color{red}{it}}\newline \end{align} $$

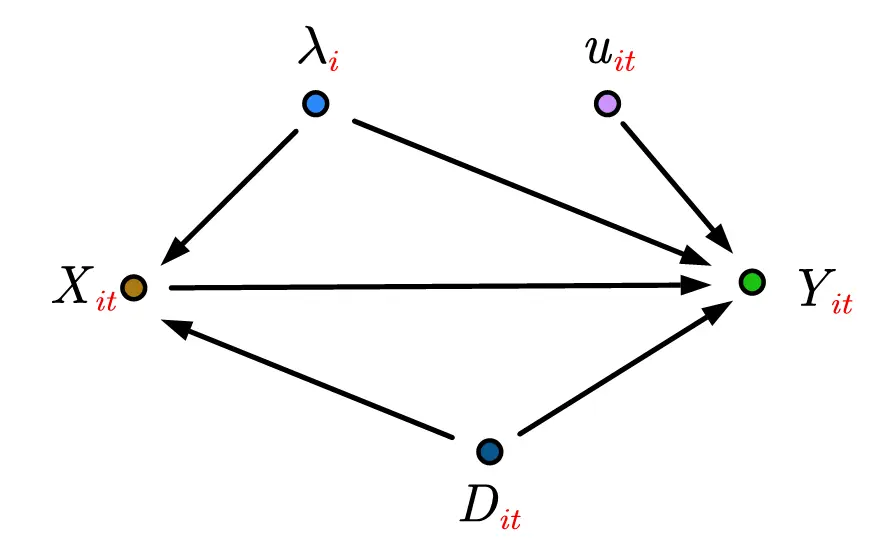
个体效应——因果关系示意图。将个体效应看做混淆因子，通过控制进行截断

$\boxed{组内估计}$，固定效应假定个体效应与解释变量相关，因此我们要利用组内离差法消除这种相关，类似去中心化——进行减去分组内组内均值的处理⁵。

平均值取同一个变量，不同年份的数值的平均: $\bar X_i = \frac{\sum_{t=n}^{t=1}{X_{it}}}{t}$

补充

面板数据的方差分析。当我们设定好了 xtset id year 后，id 可能是空间编号、也可能是行业编号、也可能是个体编号，我们就有了 n 个小组，每个组内部有有方差，就是组内方差；每组之间也有方差，就是组间方差。进行方差分析有助以确认我们研究的分组是否合适。
这里采用的组内估计的方法，比组间估计更有效。论证过程为伍德里奇计量经济学课后题，这里不再展开。

$$ Y_{\color{red}{it}}-\bar Y_{\color{red}{i}}=\alpha (X _{_{\color{red}{it}}}-\bar X _{\color{red}{i}})+\beta (M_{_{\color{red}{it}}}-\bar M _{\color{red}{i}})+(u_{_{\color{red}{it}}}-\bar u _{\color{red}{i}}) $$ 这个式子也能理解成滞后的 $\boxed{一阶差分法}$ 。 $$ Y_{\color{red}{it}}-\bar Y_{\color{red}{i}}=Y_{\color{red}{i,t}}-Y_{\color{red}{i,t-1}} =\alpha (X _{_{\color{red}{it}}}-X _{\color{red}{i,t-1}})+\beta (M_{_{\color{red}{it}}}- M _{\color{red}{i,t-1}})+(u_{_{\color{red}{it}}}- u _{\color{red}{i,t-1}}) $$ 综上，目前个体固定效应有了三种估计方程：虚拟变量最小二乘、组内估计、一阶差分。它们的估计基本上是一致的，不同点主要体现在数据假设上。一阶差分消除了个体效应，所以无法估计不随时间变化的各种效应。虚拟最小二乘法（LSDV）则要求构造的虚拟变量必须是严格外生的，而且虚拟变量太多可能导致控制变量超出 stata 的运行限制。 $$ \begin{cases} Y_{\color{red}{it}}=\alpha X_{\color{red}{it}}+\beta M_{_{\color{red}{it}}}+\sum_{1}^{N}{\alpha_{j}D_{j}}+u_{\color{red}{it}}\newline Y_{\color{red}{it}}-\bar Y_{\color{red}{i}}=\alpha (X _{_{\color{red}{it}}}-\bar X _{\color{red}{i}})+\beta (M_{_{\color{red}{it}}}-\bar M _{\color{red}{i}})+(u_{_{\color{red}{it}}}-\bar u _{\color{red}{i}})\newline Y_{\color{red}{i,t}}-Y_{\color{red}{i,t-1}} =\alpha (X _{_{\color{red}{it}}}-X _{\color{red}{i,t-1}})+\beta (M_{_{\color{red}{it}}}- M _{\color{red}{i,t-1}})+(u_{_{\color{red}{it}}}- u _{\color{red}{i,t-1}})
\end{cases} $$ 目标都是为了正确估计个体效应与控制变量相关时，被解释变量的系数$\alpha $，而且上面的四个估计式的参数$ \alpha $也相同： $$ Y_{\color{red}{it}}=\alpha X _{_{\color{red}{it}}}+\beta M_{_{\color{red}{it}}}+\lambda_{\color{red}{i}}+\color{blue}{(\gamma_{\color{red}{t}}+u^{\prime })}\ $$

*补充：Frisch-Waugh-Lovell Theorem

证明虚拟变量最小二乘、组内估计的系数 $\alpha$ 相同的引理为“Frisch-Waugh-Lovell Theorem”。
举个极简的例子：
现实的方程是： $$ Y=\beta_1 X_1+ \beta_2 X_2 +u_1 $$ 我们想要估计出 $\beta_1$，但是我们遗漏了变量 $X_1$，只回归了 $X_2$ ,得到以下式子：
$$ Y=\alpha X_2+u_2 $$ 此时我们只需要再用 $X_2、X_1$ 进行回归, 得到如下式子：
$$ X_1=\gamma X_2+u_3 $$ 最后使用残差进行回归：
$$ u_2=\dot \beta u_3+u $$ 根据已经进行的两个回归的残差，我们可以得到：
$$ \begin{cases} u_2=Y-\alpha X_2\newline u_3 = X_1 - \gamma X_2 \end{cases} $$ 展开变形，我们直接得到：
$$ Y=\dot \beta X_1 + (\alpha-\gamma)X_2+u $$ 可以发现 $\dot \beta=\beta_1$ ,通过曲线救国，间接估计，我们估计出了我们想要的系数 $\beta_1$。虚拟二乘回归就是先回归$ Y $与虚拟变量 $D$，然后回归 $X_1$ 与 $D$ ，最后使用残差进行估计，因此系数和组内估计系数回归一致。

通过 FWL 可以证明一阶差分估计和虚拟变量的估计是相等的。

如果想自己尝试，可以使用 stata 自带数据测试⁶：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


clear                            
sysuse auto  
*stata自带测试数据
reg mpg foreign weight
*现实想要回归的数据，有两个解释变量foreign和weight
reg mpg foreign
*漏掉变量weight进行回归
predict mpgResidF, residual
*生成残差
reg weight foreign
predict weightResidF, residual
reg mpgResidF weightResidF
*会发现回归系数和reg mpg foreign weight的对应weight系数相同

时间固定效应：

时间固定效应是基于个体固定效应进行添加，添加了后称为“双固定效应”。基于LSDV 法添加 t-1 个虚拟变量。

个体固定效应不随时间改变，所以可以通过一阶离差、组内估计相减去除，但时间效应很难采用相同的做法，因为个体与个体分组、排序都不明确。只能采用LSDV 法添加 t-1 个虚拟变量。

$$ Y_{\color{red}{it}}=\alpha X_{\color{red}{it}}+\beta M_{_{\color{red}{it}}}+\lambda_{\color{red}{i}}+\sum_{1}^{T}{\alpha_{j}D_{j}}+\color{blue}{u_{\color{red}{it}}} $$

如果我们假设每年时间效应相同，为固定值 $\gamma$，式子也可以简化为：

$$ Y_{\color{red}{it}}=\alpha X_{\color{red}{it}}+\beta M_{_{\color{red}{it}}}+\lambda_{\color{red}{i}}+\gamma t+\color{blue}{u_{\color{red}{it}}} $$ 再次提醒固定效应、随机效应整个分类都是重点关注个体效应带来的内生性问题。个体效应的控制是为了对抗个体特质的内生性（类似“辛普森悖论”的分组，因为用于分组的属性本身影响着我们要研究的模型），时间效应则没有这么强的干扰，所以都是在控制个体效应的基础上再控制时间效应，面板数据一般没有单独控制时间效应，不控制个体效应的做法。

3、随机效应

固定效应假设个体效应 $\lambda_{\color{red}{i}}$ 与个体相关，意思就是相同的个体分组有相同的个体效应，于是我们可以通过离差法、组内估计相减，直接消掉干扰项。随机效应与之相反，假设个体效应 $\lambda_{\color{red}{i}}$ 没有与解释变量相关，我们无法通过离差法、组内估计相减消除。

基于把残差看成截距的理解就是，在固定效应看来，每个分组共享一个截距，分组内部相减就消掉这个截距了；在随机效应看来，截距是随机的，不可能按照分组达成统一。

在操作上，类似工具变量，其实是根据残差对变量进行了加权。

要解决的问题是残差的自相关，

$$ Y_{\color{red}{it}}=\alpha X_{\color{red}{it}}+\beta M_{_{\color{red}{it}}}+\color{blue}{\lambda_{\color{red}{i}}+u_{\color{red}{it}}} $$ $\color{blue}{\lambda_{\color{red}{i}}+u_{\color{red}{it}}}$ 虽然与$ X_{\color{red}{it}}$ 、 $ M_{\color{red}{it}}$ 不相关，但是由于其具有个体效应，在面板数据中，不同年份、同一个个体是自相关的。正是自相关这点让随机效应区别于混合 OLS。

为了彻底理清这个复合残差 $\color{blue}{\lambda_{\color{red}{i}}+u_{\color{red}{it}}}$，借助广义最小二乘（GLS）变形消除序列自相关。

$$ Y_{\color{red}{it}}-\theta\bar Y_{\color{red}{i}}=\alpha (X _{_{\color{red}{it}}}-\theta\bar X _{\color{red}{i}})+\beta (M_{_{\color{red}{it}}}-\theta\bar M _{\color{red}{i}})+(u_{_{\color{red}{it}}}-\theta\bar u _{\color{red}{i}}) $$ 我们可以发现 $\theta=1$ 时，这是固定效应（FE） ； $\theta=0$ 时，这是混合 OLS。因为随机效应就是借助固定效应和混合 OLS 拆解估计随机效应的残差。

省流总结

/img/计量数据的分组与测度（STATA版）.zh-cn-20240523103328654.webp — 省流总结

面板数据必定带有时间和空间两个维度，因此混合 OLS、固定效应、随机效应是分解残差的构成。

第一个问题是回答个体效应的内生性。在固定效应的估计又有三种方法。

第二个问题是回答个体效应的自相关。

四、常用 stata 操作

1、reg 命令：经典回归

1
2
3
4
5


*混合OLS
reg Y X ,robust
*固定效应：使用虚拟变量最小二乘回归法（LSDV）
reg Y X i.id //单向固定，方法为LSDV
reg Y X i.year i.id //双向固定，方法为LSDV

2、areg 命令：优化后的 reg 命令

和 reg 的估计完全一样。由于使用 LSDV 法会产生大量虚拟变量，展示结果的表格往往会很长，areg 会用 absorb 进行固定效应，但是通过 absorb（）命令吸收不进行展现。但缺点是 absorb（）中只能放一个。

1

areg Y X i.year, absorb(id) //双固定 ，方法为LSDV

3、xtreg 命令：针对面板数据

1
2
3
4
5
6
7


xtset id year //设定个体分组和时间变量
*固定效应
xtreg Y X ,fe //单向固定，采用的方式是“组内估计”
xtreg Y X i.year ，fe //双向固定,“组内估计”的个体固定效应和LSDV的时间固定效应
sdds
*随机效应
xtreg Y X ,re //GLS,广义最小二乘估计

4、reghdfe 命令：多维固定

可以进行两个以上的固定效应控制。

1
2
3
4
5
6


*双向固定
reghdfe Y X, absorb(id year) //既然它的命令id和year能等效处理，那么我猜测估计方法依然是LSDV
*混合OLS
reghdfe Y X, noabsorb 
*交互变量的固定
reghdfe Y , absorb(year#prov) //year和prov效应的交互影响，也允许定类变量和连续性变量进行交互

5、stata 代码验证

1
2
3
4
5
6
7
8
9


*使用stata自带的xtpcse命令专用例子数据
webuse grunfeld,clear
*如果没有网络导入，可能是网络问题，需要挂梯子
*数据库站：*https://www.stata-press.com/data/r10/xt.html
*也可以直接去下载
reg mvalue invest kstock  i.company
xtreg mvalue invest kstock ,fe
areg mvalue invest kstock , absorb(company)
reghdfe   mvalue invest kstock  , absorb(company)

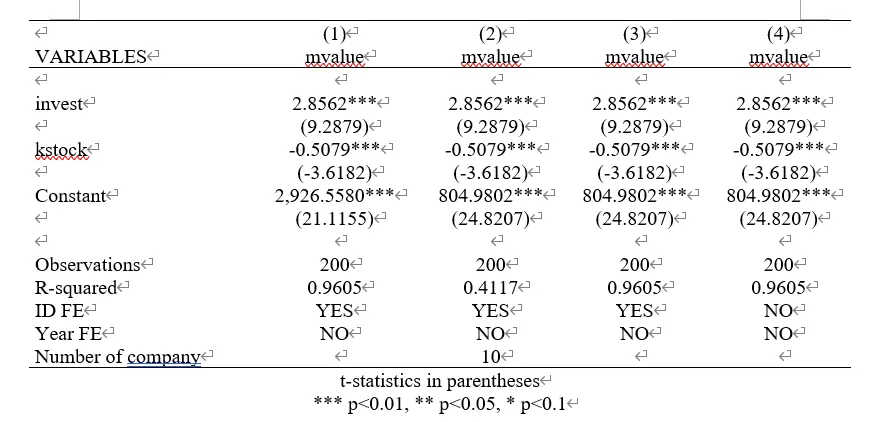
代码块分别使用了四种命令进行固定效应，固定个体效应，不固定时间效应，结果如下图，可以发现他们的系数估计是完全相同的。

为何截距部分，也就是常数项不同——并未在任何实操书中找到解答。个人认为⁷是因为各个命令计算残差方式不同影响的。

（1）混合 OLS 是计算一个回归方程与所有的点的残差。

（2）（3）（4）是聚类有了很多系数相同、截距不同的回归方程，每个点和自己对应的回归方程计算方差然后加总。
为何 $R^2$ 不同：

（1）（3）（4）都使用的 LSDV 法，所以生成了很多虚拟变量。

（2）用的组间估计，没有生产虚拟变量。

/img/计量数据的分组与测度（STATA版）.zh-cn-20240523103353234.webp — 回归表

顺便一提，当我们把代码换成如下的代码，情况也会发生改变：

1
2
3
4
5


reg mvalue invest kstock  i.company 
xtreg mvalue invest kstock ,fe r 
areg mvalue invest kstock , absorb(company)  vce(cluster company)
reghdfe   mvalue invest kstock  , absorb(company) 
xtreg laborinput did i.year, fe robust

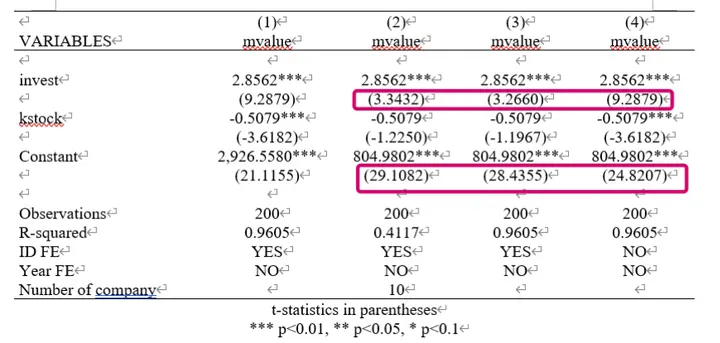
/img/计量数据的分组与测度（STATA版）.zh-cn-20240523103416018.webp — 回归表

从图片中可以看出，系数估计相同，标准差也不同。

默认回归是普通标准差，要求数据满足同方差；

添加 r, 也就是 robust 后是稳健标准差，是为了解决数据异方差；

添加 vce (cluster company) 是聚类稳健标准差，是为了解决数据异方差+内部自相关。

四、机制检验

1、机制检验在实证中的灰色地带

辛普森悖论启示我们分组回归和整体回归的结果可能完全相反，原因之一就是遗漏变量。所以我们要添加控制变量。在使用"面板数据”时，数据多了“时间”和“空间”两个维度。依然可能对研究产生影响，所以我们需要分离“个体效应”和“时间效应”。回答辛普森悖论——此时我们解决的是因果性问题，要求避免内生性。在机制检验中，有人用分组回归或者交互项回归来扩展结论，默认前提——机制检验的新变量不是你忽略的控制变量。

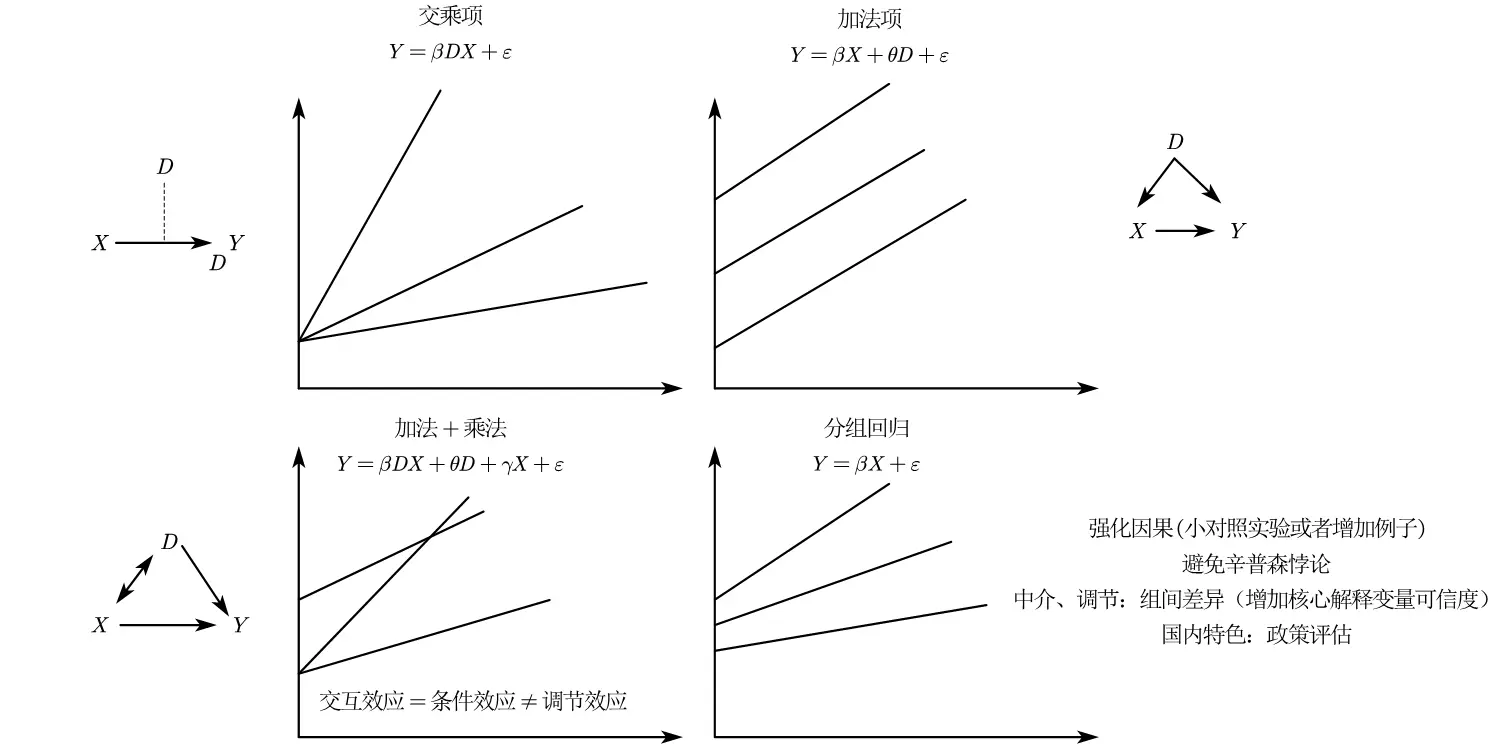
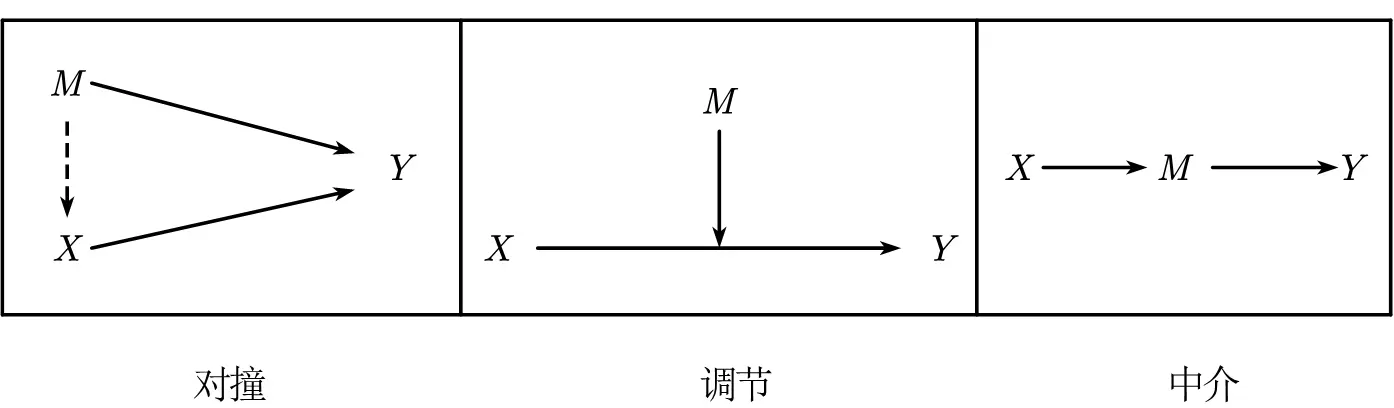
这里有个巨大的问题——在进行机制检验时，你又如何保证没有内生性呢？例如下图，最左边的是因果关系的对撞路径，右边是机制检验的调节效应、中介效应。很显然的地方在于，含有混杂因子的对撞效应依然能满足调节效应和中介效应。所以这又有了一个新的内生性问题！！！！所以朱家祥和张文睿（2021）⁸说调节效应是不满足统计学的因果关系检验的。在这基础上，江艇（2022）⁹干脆呼吁取消中介三步法，因为没有意义——这样既无法证明有内生性，也无法证明没有内生性。

于是我们的机制检验就只剩两条路可选

1. 再进一步证明没有内生性。 此时再做一个对照试验（感觉又是一个微缩的经济实证对比）；或者讨论分组回归后残差的与被解释变量的相关性。基于相关关系+理论解释去靠近因果关系。

/img/计量数据的分组与测度（STATA版）.zh-cn-20240523103507212.webp — 《因果推断经验研究中的中介效应与调节效应》江艇（2022）

2. 无需证明，我的变量是天然外生的。 变量从现实意义上来看没有内生性，也就是多扩展理论和经济意义的解释即可。国内最常见的灌水就是四大区域、胡焕庸线，因为从现实意义上来看这些分类就是天然的外生变量。

似乎机制检验似乎就是不完整的小实证，通过残缺的实证步骤大概扩展下结论。个人感觉所有的计量教材中都没有强调过所谓的“机制分析”，只是在国内成为了特定的要求。可见经济学的定量最后还是现实理论+定量各一半的分析。

2、中介效应：和心理统计的区别

中介效应这部分的观点主要参考了《为什么》（朱迪亚·珀尔）

当我们询问为什么时，回答问题的逻辑链条有两种，一种是原理、一种是过程。

$$ 吃橘子\rightarrow维生素C\rightarrow抵抗坏血病\newline 老人\rightarrow摔倒\rightarrow住院\ $$ 以上面两个路径图为例子，第一个吃维生素 C 抵抗坏血病听起来更像原理性的回答，而老人摔倒更像是过程。我见过许多论坛、社科自媒体视频认为是“经济学偷了心理学的中介效应”——实际情况并非如此。

心理学能够广泛应用中介效应，是因为心理学统计的路径图是： $外界刺激\rightarrow人体反应、激素变化\rightarrow行为变化$ ，这样的路径更像原理。经济学则只是这 $变量1\rightarrow变量2\rightarrow变量3$ 样的回答，更像一种过程描述，更加宽泛，不像心理学那样看起来贴合原理实质，所以备受质疑。心理学在选择中介变量时限定了是人体表现，经济学的变量并没有这么严格的限制，因此极易出现伪相关。例如在维生素 C 和坏血病中，人们长久以来以为是“水果——橘子”的作用，科斯特北极探险队认为重点在于水果是新鲜的，那么新鲜肉有同样的效果没有准备任何水果，最后大家都得了坏血病。

为回答“辛普森悖论”类似，我们依旧需要中介效应，因为存在“ $\boxed{中介谬误}$ ”

以 science 上发表的《Sex Bias in Graduate Admissions: Data from Berkeley》¹⁰为例，我们得到以下因果关系路径图。

性别对录取率有两个方面的影响路径。

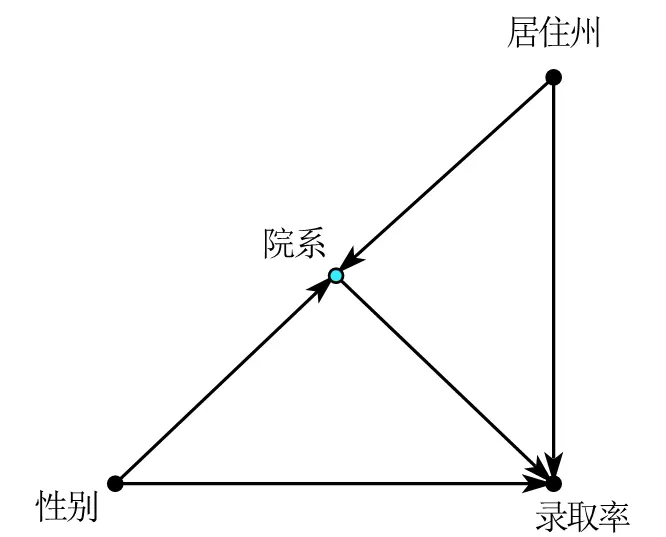
/img/计量数据的分组与测度（STATA版）.zh-cn-20240523103531814.webp — 《Sex Bias in Graduate Admissions: Data from Berkeley》

直接效应：$性别\rightarrow录取率$

间接效应： $性别\rightarrow院系\rightarrow录取率$，在间接效应中，“院系”就是中介变量。

如果我们直接将"院系"作为控制变量，此时展现的是性别-录取率的直接效应，回归会显示女性遭到了歧视。

如果我们只将“居住州”作为控制变量，此时展现的就是性别-录取的直接效应和性别-院系-录取率的间接效应，此时显示女性没有遭到歧视。截然不同的结果就是“辛普森悖论”。在咖啡中，我们犯错了是遗漏了变量；这里犯错是因为控制了“中介变量”。最终结论是，因为女生们敢于申请难度最大的院系所以看起来录取率低，所以院系是重要的中介变量并且不应该随便加以控制。

所以中介变量不应该作为控制变量，同时如果我们要区分直接效应和中介效应，是需要进一步区分的。

3、调节效应：分组回归还是交互项

发现了个超全总结

这一部分主要参考了《回归分析》（谢宇）

对于变量 $Y$ 、$X_1$ 、$ X_2$ 、$D$ 来说，我们产生了不同的估计策略。

分组回归：$Y=\beta_1 X_1+\beta_2 X_2+u$ ,然后按照 D 进行分组

引入交互项, 此时还有两种估计：

$$ \begin{cases} Y=\beta_1 X_1+\beta_2 X_2+\beta_3D+\beta_4 DX_1+u \newline Y=\beta_1 X_1+\beta_2 X_2+\beta_3DX +u \end{cases} $$

交互项和分组回归的作用区别？

一般来说，交互项强调调节效应、分组回归强调异质性，江艇（2022）认为二者是一个东西。不过，两者确实还是存在一些差别：

首先，存在必须要用分组回归的情况，当虚拟变量大于两组时，例如东西南北中区域异质性讨论，我们不可能用 1-4 来量化他们在交互项中的作用，反复采用 0-1 编号也不符合对照逻辑，此时需要分组回归。其次，存在我们需要研究交互项的情况，也就是替代效应和互补效应。当方程变为 $Y=\beta_1 X_1+\beta_2 X_2+\beta_3DX +u$ 时，研究边际效应，彼此的边际效应会受对方的影响。最后一点，当组间系数较为相似时，分组回归也会被当成一种稳健性检验。

接下来总结经常出现的几个结论看法（不过我感觉这些结论没有权威论文证实）:

统计检验交互项更好，因为有显著性检验（但是现在分组回归似乎也可以检查系数差异的显著性了），且敏感度更高，而且用的是全体样本，分组回归会减少样本量；
数据假设不同，交互项假设只有交互相关的分组存在组间差异，要求更加严格。交互项要求组与组之间控制变量系数要一致，分组回归则不要求。由此有个引申的结论——当一个变量和所有控制变量交互，交互变量估计和分组回归是完全一致的。
不同变量不同讨论，交互项可以分为虚拟变量虚拟变量（建议参考）、虚拟变量连续变量、连续变量连续变量，需要具体分析。（《计量经济学基础》（古扎拉蒂）在虚拟变量部分支持虚拟变量虚拟变量——双重差分法盛行下这点没有争议。)

交互项假设总体上机制检验这里依旧属于灰色地带。只要你的变量逻辑讲得通，分组和交互哪个用显著用哪个就行，都显著更好，就都用上。

什么样的项目适合作为交互

从数学意义来考虑，加法管截距，乘法管斜率。

/img/计量数据的分组与测度（STATA版）.zh-cn-20240523103738664.webp — 从图中可以看出，调节效应强调交互，因为和X一起影响斜率

从图中可以看出，调节效应强调交互，因为和 X 一起影响斜率。

分组回归则强调 X 的斜率是一样的，只是截距不同，不存在调节效应，更适合作为控制变量。

我们能删除低次变量吗？

也就是下面两个估计式子选哪个？我们可以在取了交互项 $XD$ 后去掉低次项 $X$、$D$ 吗？ $$ \begin{cases} Y=\beta_1 X_1+\beta_2 X_2+\beta_3 D+\beta_4 DX_1+u\newline Y=\beta_1 X_1+\beta_2 X_2+\beta_3DX_2 +u\end{cases} $$ 答案是需要带上 $\beta_3 D$，在第一个式子中，$\beta_4$ 确实是控制了 $X_1$ 和 $D$ 后的净效用。此时容易产生“共线性”，可以进行去中心化处理减去均值。因此如果是双重差分法，如果 did 和预定的时间和空间设定一致，就变成了要求双向固定效应。

以上参考来自¹¹

交互项最多能几个相乘?

一般不超过三个。原因是三个以内更符合直觉性的对照试验，三个以上后作者难以解释对照实验结论。

参考资料：

《计量经济学导论》（伍德里奇）

《计量经济学基础》（古扎拉蒂）

《基本无害的计量经济学》（安格里斯特 / 皮施克）

《因果推断实用计量方法》 (邱嘉平)

《高级计量经济学及 Stata 应用》（陈强）

《回归分析》（谢宇）

《为什么》（朱迪亚·珀尔）

计量回归中的交互项到底什么鬼? 捎一本书给你

计量经济学中"交互项"相关的5个问题和回应

Stata: 交叉项\交乘项该这么分析！

Stata：交乘项该如何使用？

Stata：边际效应分析

Stata：图示连续变量的边际效应(交乘项)

Stata：图示交互效应\调节效应

加入交乘项后符号变了!?

Anwar S, Fang H. An alternative test of racial prejudice in motor vehicle searches: Theory and evidence[J]. American Economic Review, 2006, 96 (1): 127-151. ↩︎
每每看到各类书用这个例子引出因果关系，总是感觉时间飞逝 ↩︎
Judea Pearl 在他的著作《the book of why》中支持这一点。书中第六章是从平均值比例数出发引出辛普森悖论 ↩︎
陈强高级计量教材中说也可以理解为“个体效应被平均掉了” ↩︎
下面这个使用去中心化的式子，写最终结果时伍德里奇教材的第六版好像写错了残差的符号，陈强教材是正确的。 ↩︎
参考代码来自哈佛商学院的课程资料 https://www.hbs.edu/research-computing-services/Shared%20Documents/Training/fwltheorem.pdf ↩︎
欢迎质疑。 ↩︎
朱家祥, 张文睿. 调节效应的陷阱[J]. 经济学 (季刊), 2021,21 (05): 1867-1876. DOI: 10.13821/j.cnki. Ceq. 2021.05.19. ↩︎
江艇. 因果推断经验研究中的中介效应与调节效应[J]. 中国工业经济[2023-12-28]. ↩︎
P. J. Bickel et al. ,Sex Bias in Graduate Admissions: Data from Berkeley. Science 187,398-404 (1975). DOI: 10.1126/science. 187.4175.398 ↩︎
Cleary P D, Kessler R C. The estimation and interpretation of modifier effects[J]. Journal of Health and Social Behavior, 1982: 159-169.12: ↩︎