审查员设计(Judge IV):一种随机分配的因果推断
在混乱之中发现单纯 ——爱因斯坦
大自然充满了魔力,随机分配让准自然实验成为可能,其也是因果推断的发源基石之一1。一般认为,随机分配会平均掉和解释变量相关的偏差,进而得到具有良好特性的实验组和对照组。在 2022 年,一种基于随机分配的工具变量思想逐渐频繁登上了 top5 经济期刊。
发展历程
举一个例子:
- 大型社会考试时我们会祈祷遇上仁慈的改卷老师。
- 贷款时我们会祈祷遇上宽松的审查员。
- 旅游时我们祈祷期待遇上好心的路人。
命运的随机分配充满了魔力,一些人确实被随机分配到了更为仁慈的审查员手里,于是他们的命运,相较于哪些随机分到了严格的审查员的人群产生了差异。这就是 Judge_IV 的核心因果思想,先量化这些审查员的严格程度。然后比较随机分配到他们手中的群体的未来发展差异,进而成为一种基于随机分配的因果推断。
Judge leniency IV designs: Now not just for Crime Studies ——David McKenzie
JUDGE – IV,也可以叫 Examiner Designs (审查员设计),或者 Judge leniency IV designs(仁慈法官工具变量)。这类工具变量的思想先起源于描述统计,当时有人统计了不同教师和不同法官的给分和判案倾向,发现了显著的差异性。2006 年有文章直接使用了这个工具变量作为检验。
工具变量的构造非常检验,和其他工具变量的构造类似2——去中心化的均值期望。
2018 年以后,不断有研究拓展了这种方法。这种测量关注的是审查员的严格程度。简单来说就是 {通过,不通过} 的概率。去中心化的数学期望分布在 0-1 之间,用于衡量严格程度。
也就说,只要拥有随机分配的审查员和结果方向性,就可以尝试使用 judge iv 。例如家暴调查员是否选择带走孩子;美国的救护车公司是随机分配的,但他们的价格有高有低,在救援中会造成不同影响;房贷审查员有些人比较粗心,很容易就通过贷款申请……
实证分析
- 定义解释变量 $D_i$ : 代表审查员的变化方向,通过为 1,不通过为 0。
- 定义工具变量 $Z_{a_{\{-i\}} }$ : 代表审查员除去当前案子的其他案子的通过率。
两阶段回归便是:
$$ \text{一阶段:}D_i=Z_{a(-i)}\pi+\nu_i $$ $$ \text{二阶段:}Y_i=\alpha+\delta D_i+\epsilon_i $$
随机分配到不同倾向性审查员后的被审查对象的 发展差异。
工具变量写成矩估计的形式可以看作一种样本权重(GMM 框架下特殊的矩条件),而在这里比较的就是那些被分配到相似严格程度的法官的行为差异。这种情况也类似样本匹配的功效。
一般 iv 无法检验变量的排他性和单调性,只能通过理论阐述进行补充,但 jugeiv 的优势是它能够通过实验设计检验工具变量的单调性、排他性3。
随机分配
例子一
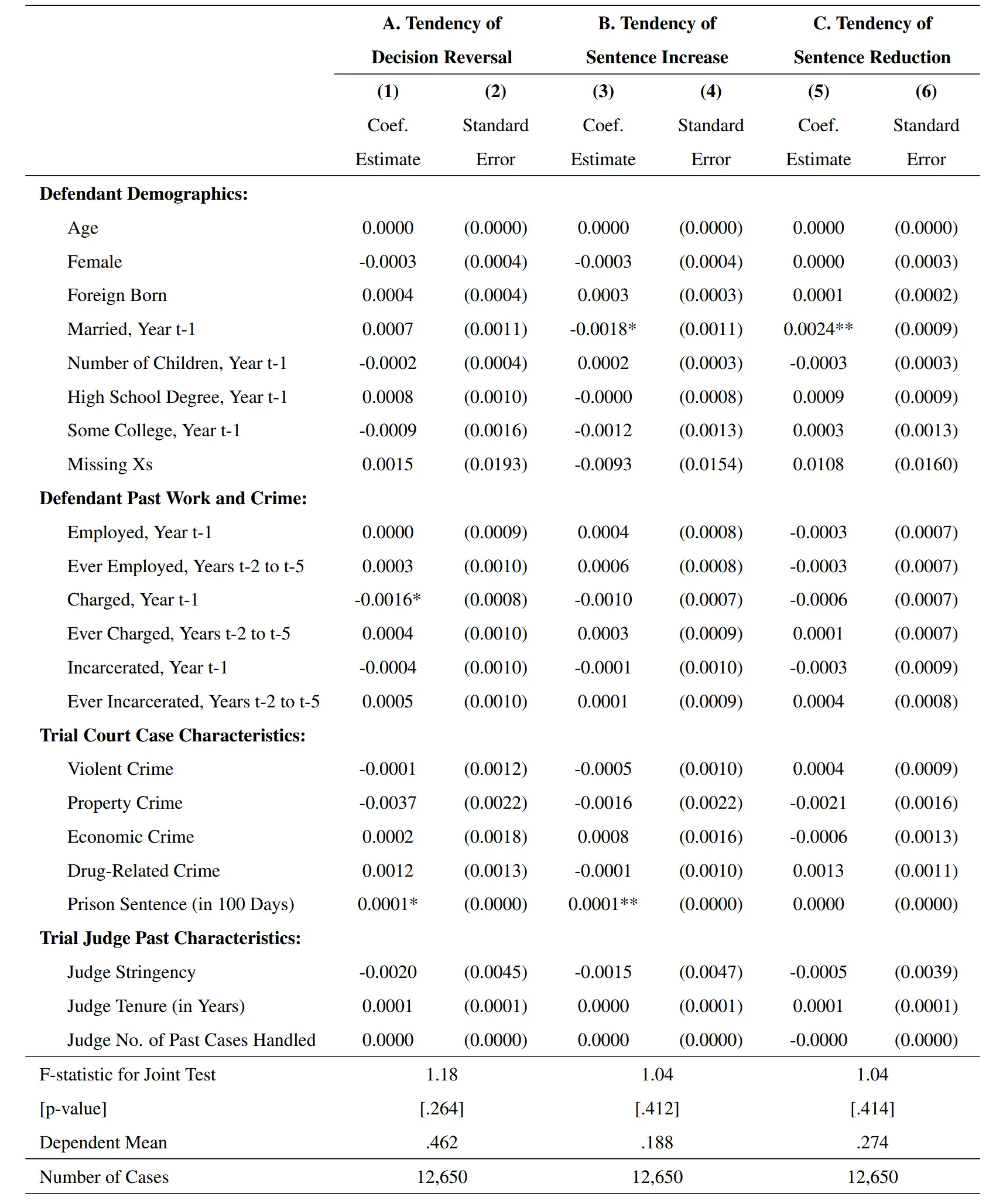
使用工具变量或者解释变量对样本特征进行回归,不显著,或者 F 检验不通过,则说明样本特征并没有干预解释变量,也就是解释变量是外生的。
在《Feedback and learning: The causal effects of reversals on judicial decision-making》中,作者通过案件的逆转方向(工具变量)对案件特征变量进行回归,皆不显著,验证了随机分配。也就说案件的结果和法官的特征是无关,每一个案件被随机分配到了不同的法官手中。
随机分配也证明了工具变量的排他性。法官随机抽取一个案件然后判案,断绝了法官自身性格因素以外情况(例如权钱交易)。
上面是使用解释变量对其他特征进行回归,通过 F 检验检验随机分配。
例子二
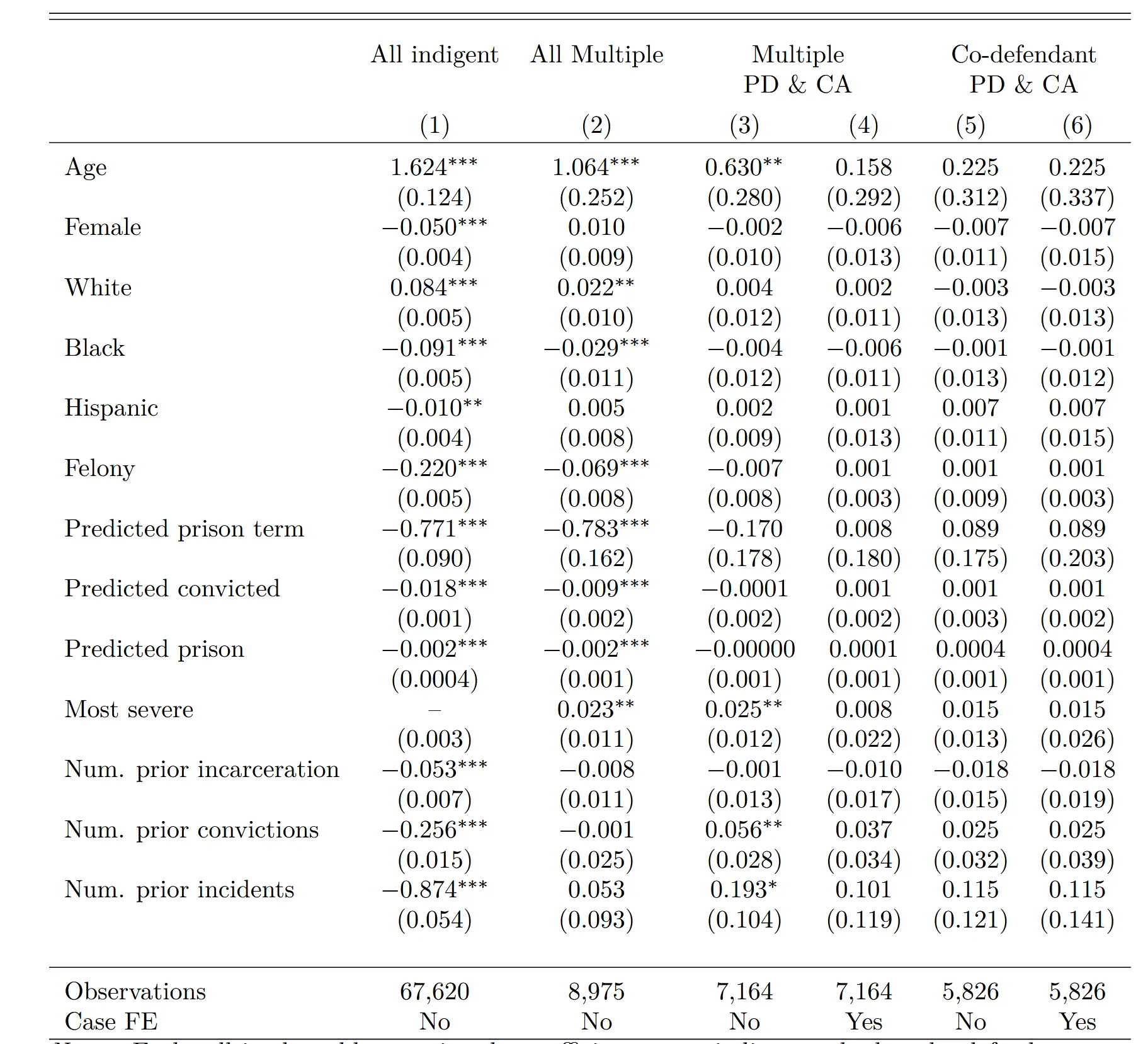
下面这篇 2025 年斯隆奖获奖的博士论文研究的就是律师的随机分配,贫穷的被告会被随机分配到公共组织和私人组织的辩护律师。将律师特征作为工具变量对分配类型进行回归,经济系数接近于 0 且不显著,说明组间差异不大进而说明随机分配。
一阶回归可视化
单调性检验方法 1:平均单调
一阶段回归同时检验了单调性与相关性。
$$ \text{一阶段:}D_i=Z_{a(-i)}\pi+\nu_i $$
代码思路是,先使用 fwl 定理,让解释变量、工具变量分别对固定效应等控制变量做回归,对残差进行标准化,再使用残差进行局部线性拟合(stata 命令为 lpoly)。
《EXAMINER AND JUDGE DESIGNS IN ECONOMICS: A PRACTITIONER’S GUIDE》结果如图。研究的是不同倾向性法官与是否选择监禁的关系。
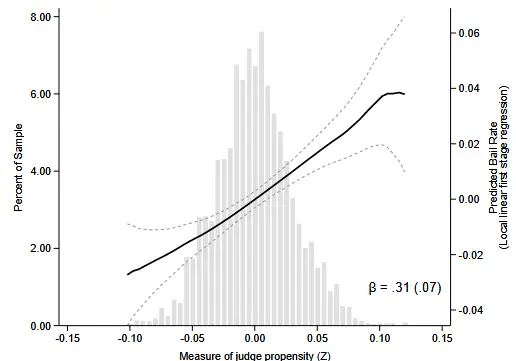
横坐标是标准化后的工具变量残差,衡量了审查员的严格程度。纵轴是对应的解释变量(具体时事件的审查结果)的残差。局部拟合呈现正相关的直线形状,通过检验。这种检验一般使用的是二次多项式局部回归。
答案是不能——正相关和较为平滑的直线趋势缺一不可。
拟合系数为正,代表着,一个案件被分到更严格(仁慈)的审查员手中,不通过(通过)的概率与之相对越高。越后方的拟合系数必须高于前方的拟合系数,才能说明仁慈法官手中通过的案件到严格法官手中是不容易被通过的。
系数为正不但验证了解释变量和被解释变量的相关性,还验证了法官之间案件通过率的单调性。
单调性检验方法 2:多峰偏好
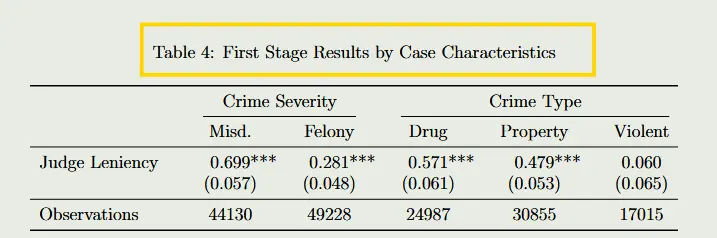
法官不能对一些类型的案件严格,另一些类型的案件宽松。可以尝试分类案件类型和案件严格程度进行一阶段回归的检验。《JUDGING JUDGE FIXED EFFECTS》演示的分组角度是案件类型和案件严重程度。
仍值得探讨的地方
- Juge iv 的构造非常简单,但具体场所是否能使用4,怎样检验依旧值得讨论。尤其是工具变量的单调性。
- 审查员设计必须是离散变量吗?不能是连续变量名?如果引入负权重会怎样影响估计结果5?
- 如果一个事件有多个审查员呢?6
- Juge iv 的渐进性要求体现在哪里?该聚焦被审查者次数还是审查员的工作次数?个人认为两者的样本规模都很重要。
是不是很多人都有过这样的想法?若是某时某刻碰见了其他的人,我们的人生是否会变得不同?随机分配总会让我思考偶然与必然的关系。偶然中的必然——必然有人中彩票,只是那个人偶然是你。在知晓随机分配之后?我们又该如何看待命运?对于一个人来说,他该选择偶然的上限?还是平均值的下限7?
推荐参考资料
课程资料
就目前而言,judgeiv 期刊论文以外的参考资料相对较少:
个人格外推荐关注他们的计量技术主题专栏。
AER 关于 jugeiv 的一些论文讨论
- Monotonicity among Judges: Evidence from Judicial Panels and Consequences for Judge IV Designs(AER, 2026)
- Judging judge fixed effects(AER, 2023)
-
我们可以从最优化和因果推断两条线审视计量的发展。最优化是关于如何增强测量的一致性,因果推断是让我们思考如何设计实验过程。 ↩︎
-
找工具变量的一些思路:关系之关系、遥远的历史变量、平均化、增长率,以及前面几类方法的组合。例如移动份额法工具变量 shift-share 就是去中心均值加上增长率。 ↩︎
-
所有的计量检验都是检验必要条件而非充要条件。 ↩︎
-
目前较为成熟的检验场景是司法数据,但其他场景的范式依旧没有定论。 ↩︎
-
Bhuller M, Sigstad H. 2SLS with multiple treatments[J]. Journal of Econometrics, 2024, 242(1): 105785. ↩︎
-
Chyn E, Frandsen B, Leslie E C. Examiner and Judge Designs in Economics: A Practitioner’s Guide[R]. National Bureau of Economic Research, 2024. ↩︎
-
其实这些方面更相关的是不确定性理论。 ↩︎