客观赋权：PCA、CRITIC、EWM、COV

 收录于 软件工具  经济学习 和 Stata 实证工具
 约 5800 字 预计阅读 12 分钟 - 次阅读  
/img/客观赋权：PCA、CRITIC、EWM、COV.zh-cn-20250114152517555.webp
目录

虎扑流行“我来发图，你们来打分”。经济学也经常赋权建立指标进行打分比较。目前互联网上的教程似乎都是“代码-数据-推导”的三缺一，这里打算一口气把三个部分通通概括。

本文先讲讲中文期刊最常见的三种“熵权法”“变异系数法”“主成分法”。以后用了其他方法将继续在本文补充。

一般赋权方法大赏（图源：http://www.huaxuejia.cn/ism/CESAISM/coupling-coordination.php）
一般赋权方法大赏（图源：http://www.huaxuejia.cn/ism/CESAISM/coupling-coordination.php）

一、“标准化”和“归一化”

这部分主要参考了下面这篇博客：

为什么耦合协调度的论文绝大部分是算错的？

$\boxed{ 无量纲化 }：$ 无论最初我们有多少奇奇怪怪的指标，我们最后拿出手需要是一个没有“单位”的总分，这个过程就叫做无量纲化。

$\boxed{ 规范化 }：$ “标准化”和“归一化”都是为了把数据规范化，将数据进行缩放，处理成我们想要的形式，同时尽可能地保留数据的比较排序特征。

$$ \small A>B>C>0\xrightarrow{规范化}\frac{A}{A+B+C}>\frac{B}{A+B+C}>\frac{C}{A+B+C} $$

“归一化”处理的是数值范围，“标准化”处理的是数值分布。不改变比较排序特征是因为他们都是线性变化。

1、归一化（Normalization）

把数据变化到特定的范围，消除不同单位、数字间差距对分析权重的影响。

经济学常用的处理公式如下

$$ \small \begin{cases} X_{正指标}=\frac{X_{ij}-\min X_j }{\max X_j-\min X_j}\newline X_{负指标}=\frac{\max X_j-X_{ij}}{\max X_j-\min X_j} \end{cases}\in\{0,1\} $$

范围被限定为了（0,1）, 同理要把范围限制到某个区间——（a, b），那么变形就是：

$$ \small f(x)\in\{0,1\} \xrightarrow {变形} (b-a)f(x)+a \in \{a,b\} $$
  • 提示 1：正向指标和负向指标是不同的公式，需要区别处理
  • 提示 2：还有其他的规范化方法

图源：http://www.huaxuejia.cn/ism/CESAISM/coupling-coordination.php
图源：http://www.huaxuejia.cn/ism/CESAISM/coupling-coordination.php

1-1、归一化 stata 代码

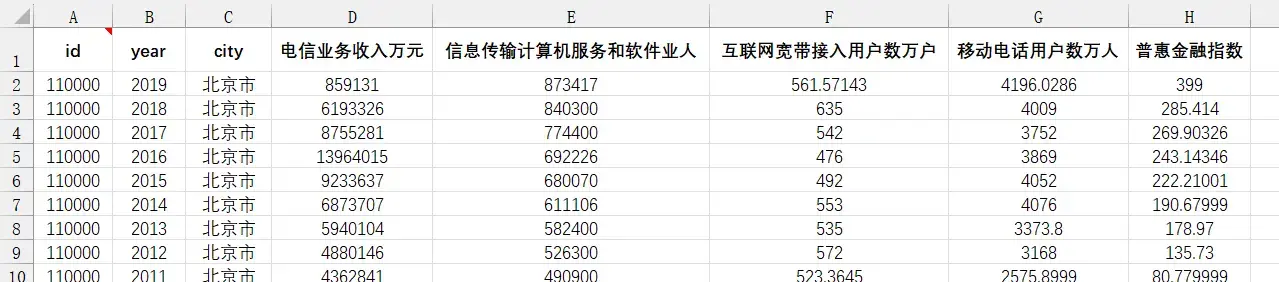
这里提供练习数据，数据源是赵涛等人（2020）的数字经济指标1。

百度网盘

面板数据，五个指标衡量数字经济|542
面板数据，五个指标衡量数字经济|542

面板数据，五个指标衡量数字经济

有很多途径可以实现极差法的归一化。

方法一：Norm 指令组

1
2
3
4

ssc install norm //指令安装
norm x1 x2 x3 , method(mmx) 
* 对应是计算方法是：[Xi - X(min)]/ [X(max)-X(min)]
* 如果想要一个截面一个截面的分组标准化，名字则为 norm x1 x2 x3, by(year) method(mmx)

这个命令的缺点是，mmx 只提供了正向指标的线性变化，不能用于负向指标。

也就是只有 $\small X_{正指标}=\frac{X_{ij}-\min X_j }{\max X_j-\min X_j}$ 的变化，没有负指标 X 负指标$\small X_{负指标}=\frac{\max X_j-X_{ij}}{\max X_j-\min X_j} $的变化。

理论上也有解决方法：通过 $1-x_{负向指标}、\frac{1}{x_{负向指标}}$ 的变形把负向指标转化为正向指标再统一执行。

提醒：所有数据最后是打分，都需要为正。

方法二：循环加分组（通用）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

*定义正向指标与负向指标

global positive_var x1  x3 x4 x5 x6  x8 x9 x10 

//定义正向指标，把x1 x3 x5 x7都打包到positive_var

global negative_var x2 x7  

//定义负向指标，把x2 x4 x6 x8都打包到negative_var

global xlist x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 

//把上述的所有指标都打包到xlist

*标准化

foreach i in $positive_var {
    qui sum `i'
    gen x_`i'=(`i'-r(min))/(r(max)-r(min)) //正向指标标准化处理
    replace x_`i'=0.000001    if x_`i'==0  //避免出现0值
  }  

foreach i in $negative_var {
    qui sum `i'
    gen x_`i'=(r(max)-`i')/(r(max)-r(min)) //负向指标标准化处理
    replace x_`i'=0.000001 if x_`i'==0    //避免出现0值
  }

2、标准化（Standardization）

$\boxed{Z-score}:$ 中心极限定理告诉我们分布函数会趋于正态分布，我们常用的是概率统计里的标准正态化。

$$ \begin{cases} X_{正指标}=\frac{x-\mu}\sigma \newline X_{负指标}=\frac{\mu-x}\sigma \end{cases} $$

2-1、标准化 stata 代码 

1
2
3

zscore x1
* 标准化后的变量为命名为z_x1
* 负向指标需要在变形后再在前面加个负号

什么时候需要标准化和归一化呢？

省流：对机器学习来说，具体对象具体诉求具体使用，对于经济学来说，无脑使用问题不大。

二、熵权法（EWM）

1、理论步骤

首先是保证数据都已经归一化，都大于 0。

$$ \small \begin{cases} X_{正指标}=\frac{X_{ij}-\min X_j }{\max X_j-\min X_j} \newline X_{负指标}=\frac{\max X_j-X_{ij}}{\max X_j-\min X_j} \end{cases}\in\{0,1\} $$

然后就是根据信息熵的定义确定权重（论文《A mathematical theory of communication》）2。

图源:《A mathematical theory of communication》（shannon,2001）
图源:《A mathematical theory of communication》（shannon,2001）

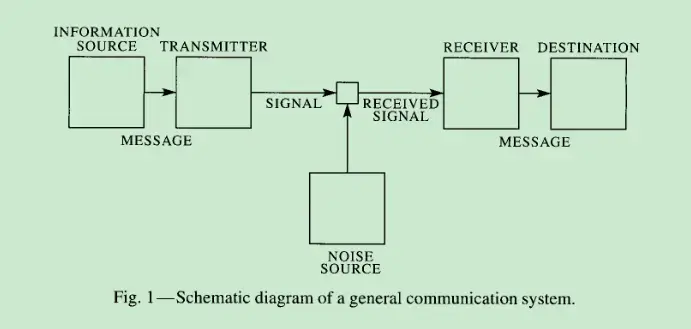
熵实际是对随机变量的比特量和顺次发生概率相乘再总和的数学期望3。

信息熵的计算为：

$$ \mathrm{E_{j}=-\frac{1}{\ln n}\sum_{i=1}^{n}p_{ij}\ln p_{ij}} $$

$p\_{ij} $就是每个样本在总体指标下的占比

$$ p_{ij}=\frac{X_{ij}}{\sum_{i=1}^{n}X_{i}} $$

当 $p_{ij}=0$ 时不适用这个式子，可以在归一化时直接把为 0 的数值进行补充。

最后得出指标权重

$$ W_{i}=\frac{1-E_{i}}{k-\sum E_{i}}(i=1,2,\ldots,k) $$

2、熵权法 stata 代码 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

*Step0:定义正向指标与负向指标

*定义正向指标与负向指标

global positive_var x1 x3 x5 x7

//定义正向指标，把x1 x3 x5 x7都打包到positive_var

global negative_var x2 x4 x6 x8

//定义负向指标，把x2 x4 x6 x8都打包到negative_var

global xlist x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 

//把上述的所有指标都打包到xlist

*标准化

foreach i in $positive_var {
    qui sum `i'
    gen x_`i'=(`i'-r(min))/(r(max)-r(min)) //正向指标标准化处理
    replace x_`i'=0.000001    if x_`i'==0  //避免出现0值
  }  

foreach i in $negative_var {
    qui sum `i'
    gen x_`i'=(r(max)-`i')/(r(max)-r(min)) //负向指标标准化处理
    replace x_`i'=0.000001 if x_`i'==0    //避免出现0值
  }
 
 ************************************熵权法*****************************************//
*Step2:计算第j项指标下第i个样本值占该指标所有样本值之和的比重Pij
foreach i in $xlist {
    egen `i'_sum=sum(x_`i')  //把每个指标进行加总
    gen y_`i'=x_`i'/`i'_sum  
  }

  gen k=_N  //这个代码可以根据数据类型做更改

foreach i in $xlist {
    gen y_lny_`i'=y_`i'*ln(y_`i')  //指标比重乘以ln(指标比重)
  }

*Step3:计算第j项指标的信息熵ej
foreach i in $xlist {
    egen y_lny_`i'_sum=sum(y_lny_`i')  //对指标比重乘以ln(指标比重)进行求和
  }

foreach i in $xlist {
    gen e_`i'= -1/ln(k)*y_lny_`i'_sum
  }

*Step4:计算信息熵冗余度dj
foreach i in $xlist {
    gen d_`i'= 1-e_`i'  
  }

*Step5:计算评价指标权重wj
egen d_sum = rowtotal(d_*)
foreach i in $xlist {
    gen w_`i'= d_`i'/d_sum
  }

*Step6:计算综合得分s
foreach i in $xlist {
    gen Score_`i'= w_`i'*x_`i'   //权重乘以标准化值
  }

egen Score=rowtotal(Score_*)   //求和
******************************************************************

三、变异系数法 （COV）

1、理论步骤

省时省力，变异系数变异系数$\boxed{变异系数} $就是每组的 标准差均值标准差均值$ \frac{标准差}{均值}$ 。

计算每个指标内部的变异系数，然后把每组指标的变异系数占比作为权重。

$$ v\_i=\frac{\delta}{\bar x\_{i}} $$$$ w\_i = \frac{v\_i}{\sum \_{i}^{n} v\_i} $$

2、变异系数法 stata 代码 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

*Step0:定义正向指标与负向指标

*定义正向指标与负向指标

global positive_var x1 x3 x5 x7

//定义正向指标，把x1 x3 x5 x7都打包到positive_var

global negative_var x2 x4 x6 x8

//定义负向指标，把x2 x4 x6 x8都打包到negative_var

global xlist x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 

//把上述的所有指标都打包到xlist

*标准化

foreach i in $positive_var {
    qui sum `i'
    gen x_`i'=(`i'-r(min))/(r(max)-r(min)) //正向指标标准化处理
    replace x_`i'=0.000001    if x_`i'==0  //避免出现0值
  }  

foreach i in $negative_var {
    qui sum `i'
    gen x_`i'=(r(max)-`i')/(r(max)-r(min)) //负向指标标准化处理
    replace x_`i'=0.000001 if x_`i'==0    //避免出现0值
  }
************************************变异系数法*****************************************
*Step2:计算变异系数
foreach i in $xlist {
egen sd_`i'= sd(x_`i') //计算标准差
}

foreach i in $xlist {
egen mean_`i'= mean(x_`i') //计算平均值
}

foreach i in $xlist {
gen v_`i'= sd_`i'/ mean_`i' //计算变异系数
}

egen v_sum = rowtotal(v_*) //变异系数加总

*Step3:计算各指标权重
foreach i in $xlist {
gen w_b_`i'=v_`i'/v_sum  
}

*Step4:计算综合得分
foreach i in $xlist {
   gen Score_b_`i'= x_`i'*w_b_`i'
}
egen Score_b=rowtotal(Score_b_*)

个人感觉对比下来变化差异不大

数字经济指标，个人找数据补到了2021年，额外进行了分组绘图。（左变异系数、右主成分法，总体排序基本是稳定的）
数字经济指标，个人找数据补到了2021年，额外进行了分组绘图。（左变异系数、右主成分法，总体排序基本是稳定的）

四、CRITIC 法

待补

五、主成分得分 （PCA）

1、理论步骤

可参考如下文章，他们都讲的非常精彩。

主成分分析（PCA）原理详解

CodingLabs - PCA的数学原理

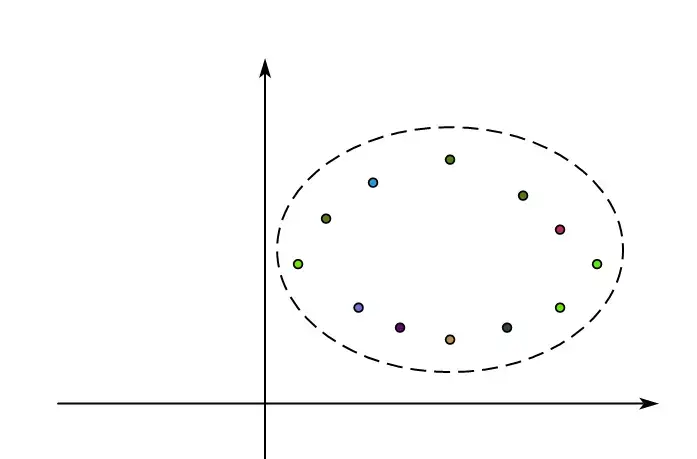
为了进一步形象化概括，我们可以用二维数据来展示 pca 分解的过程4。

当数据标准化（标准正态分布）后，我们会得到呈现椭圆形的数据集。

数据集
数据集

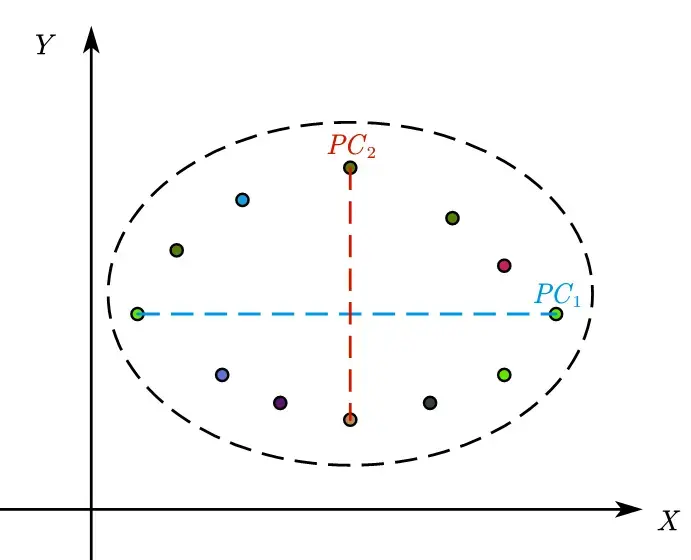
此时我们画一个平行于 x 轴的线，使它对应的方向上具有最大方差，此时这个主成分 $PC_1$ 就是两者的线性组合。

$$ PC_1=a_{11}X_1+a_{12}X_2 $$

分解
分解

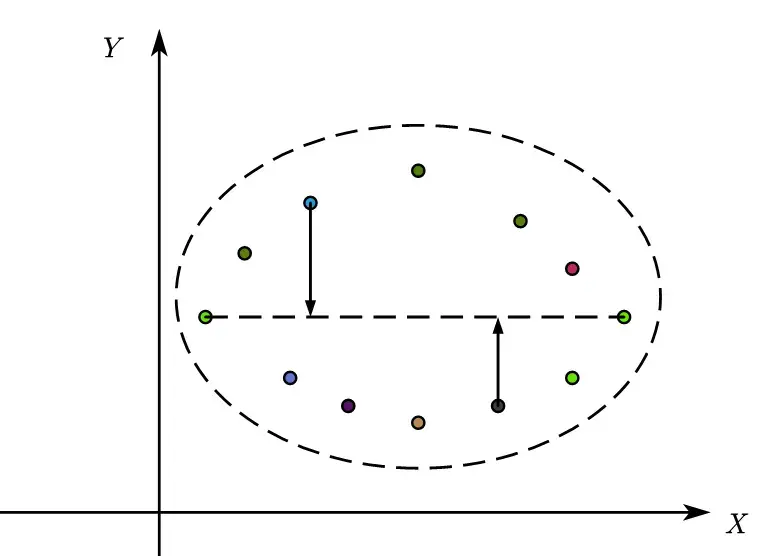
同理，我们再画平行于 y 轴的线，同时注意到y 轴与 x 轴是垂直的，这样才能保证两个主成分之间是无关的。

y轴与x轴是垂直的，这样才能保证两个主成分之间是无关
y轴与x轴是垂直的，这样才能保证两个主成分之间是无关

有 n 个指标就是 n 维空间，也就有 n 个互相垂直的方向

  • $\boxed{特征向量}：$ 特征向量是方差最大（信息最多）的轴的方向，称之为主成分。

  • $\boxed{特征值}：$ 特征值为某个主成分的方差，其相对比例可理解为方差解释度或贡献值。特征值从第一主成分会逐渐减少。

  • $\boxed{载荷}：$ 载荷是特征向量乘以特征值的平方根。载荷是每个主成分上各个原始变量的权重系数。

  • $\boxed{维度}：$ 维度在数据中就是几个指标。有 n 个指标就是 n 维空间，也就有 n 个互相垂直的方向，也就是 n 个可以分解的主成分，但我们在操作中只需要部分贡献大的，所以取 k 个。从 n 到 k，这个过程就是 $\boxed{降维} $。

$$ \small \begin{cases} 指标样本1\newline ...\newline 指标样本n \end{cases} \xrightarrow{降维} \begin{cases} PC_1=\alpha_1\times f_1+\alpha_2 \times f_2 +...\alpha_3 \times f_n\newline ...\newline PC_k=\beta_k \times f_1+\beta_2 \times f_2 +...\beta_n \times f_n \end{cases} $$

2、主成分法 stata 代码

分为两部分，一部分是得出分数的必要操作，一部分是非必要的画图操作。

注意事项！！！！！！！！！！！！

  • stata 的 pca 命令自带数据规范化，不需要额外预处理操作
  • 分析数据的负向指标需要自己正向化：$\small 1-x_{负向指标} 、\small \frac{1}{x_{负向指标}}......$
  • 主成分法给出的是主成分 $PC_k$ ,也就是 n 个指标分解成了 k 个主成分，然后加总给出总分。原始指标没有权重。

必要操作部分：

先做预处理检验数据是否适合使用主成分分析

这些检验一般也没必要在论文里说明

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

//相关系数分析，一般大于0.4即可
//相关系数高，说明n个指标有些重复信息，这样才有降维分解成k个的价值

pwcorr_a x1-x4

*step1：进行KMO和Bartlett检验：
*球形检验，也就是理论部分提到的椭圆形好分解特征向量的方向

factortest x1-x4

//其中若Bartlett值显著（P值接近0）；且KMO值大于0.5，则可以使用主成分分析。

通过检验后，开始进行主成分分解

PCA 命令自带规范化处理。

1
2
3
4
5
6

pca x1-x4

* Eigenvalue :特征值 
* Proportion ：贡献率
* Cumulative：累计贡献率
* Comp 特征向量、载荷矩阵

数据源就是前文附件的excel:《数字经济、创业活跃度与高质量发展——来自中国城市的经验证据》
数据源就是前文附件的excel:《数字经济、创业活跃度与高质量发展——来自中国城市的经验证据》

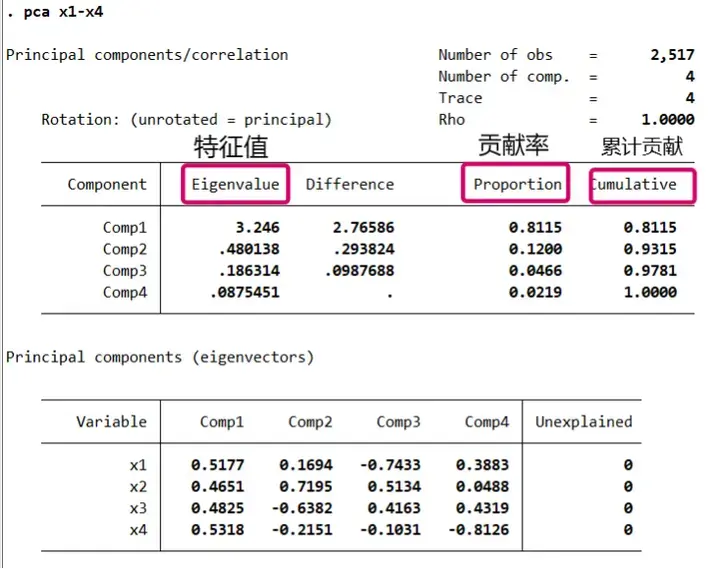
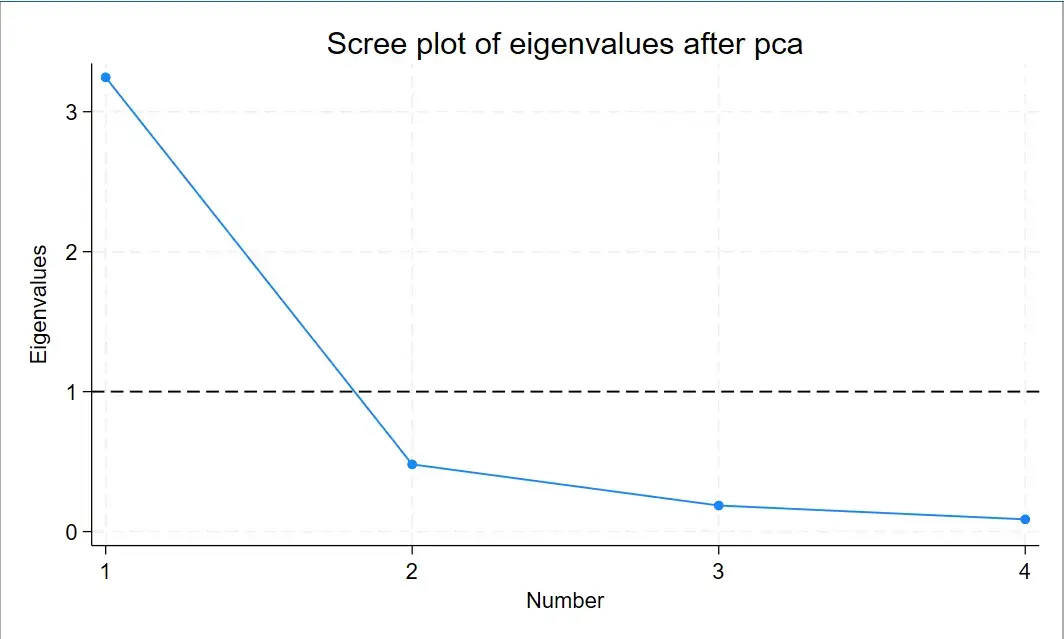
一般要求特征值要大于 1，小于 1 的话说明特征变量的解释能力还不如原变量。若三个变量特征值均大于 1，则要提取的主成分有三个。图中大于 1 的只有一个，说明我们只需要提取一个主成分。

我们也可以通过画图来展示以上结论，这个图就是碎石图。

1
2

screeplot,yline(1) 
*碎石图，选出大于1的对应主成分

碎石图，选出大于1的对应主成分
碎石图，选出大于1的对应主成分

1
2
3
4
5
6
7
8
9

*step4计算主成分得分
predict f1
*这里我们只需要1个主成分所以只需要生成f1

rotate,promax(3)factors(12) //旋转分解方向,promax(3)的（3）是旋转方式，（1）我们需要几个主成分

*step5：使用综合指标
//按照个主成分的方差贡献率占所提取的主成分的累计方差贡献率的比重，生成综合性指标。
//Score=(方差贡献率/累计方差贡献率)*f1+(方差贡献率/累计方差贡献率)*f2+......(方差贡献率/累计方差贡献率)*fn

结果
结果

由于我们只需要一个主成分，所以最后得到总分：

1
2
3

gen score = 0.8115/0.8115*f1

* 如果存在小于0的score就自己sum一下然后整体加个常数保证全部大于0就行

假设我们分析得到需要两个主成分，那么总分的式子就应该变为

1

gen score = 0.8115/0.9315*f1+0.1200/0.9315*f2

必要部分完成，接下来是非必要部分，也就是因子分析和得分图分析

非必要部分

假设我们有四个指标，四个指标特征值都大于 1，也就是我们四个主成分都可以用，也就可以通过得分图来聚类。

1
2
3
4
5

predict f1 f2 f3 f4
 scoreplot,combined factors(4)mlabel(city) yline(0) xline(0)
*mlabel是选定描述统计量名称
*factors(4)是要前几个主成分，然后两两排列来展现
*两个节点距离越近说明越相似

得分分析
得分分析

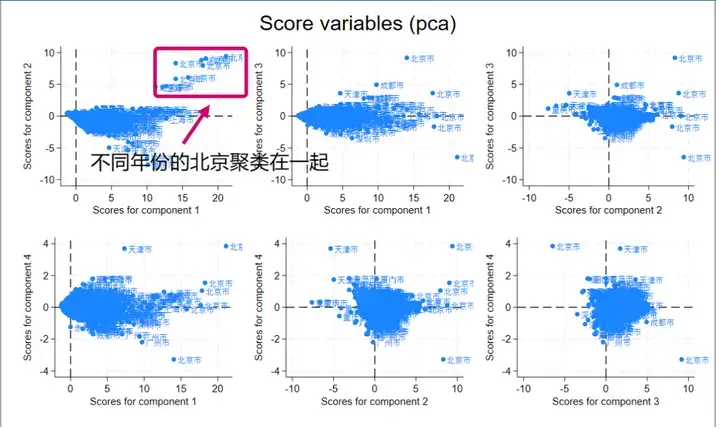
对于得分图来说，距离越近越相似，由于我们选择了参数 factors （4），那么四个主成分两两组合，就会产生 $C_4^2=6$ 个得分图。我们使用的是面板数据，我们按照的地域标签，确实可以看出**不同年份的同一个城市（北京、重庆）**总是聚类在一起。

因子载荷图命令如下：

1
2

loadingplot, factors(4) yline(0) xline(0) //荷载图
*factors(4)也是分析几个因子的设定。

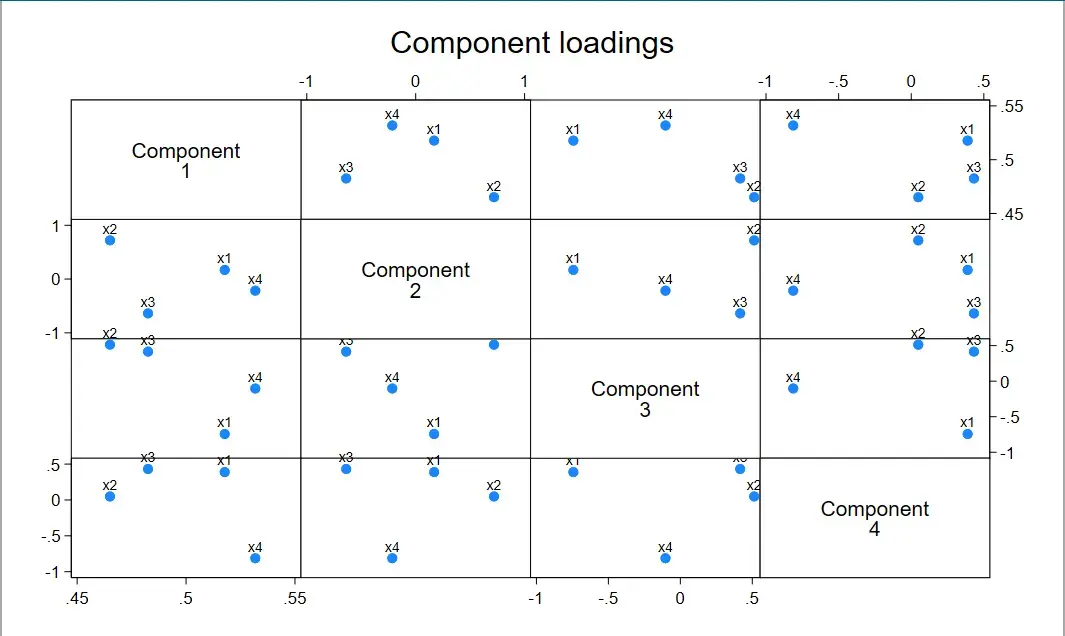
由于我们选择了参数 factors （4），那么四个主成分两两组合，就会产生 $C_4^2=6$ 个因子载荷图

它反映了不同组成分下指标的聚类程度。

因为是对称的，所以只看一侧就行，也就是有6个图
因为是对称的，所以只看一侧就行，也就是有6个图

因为是对称的，所以只看一侧就行，也就是有 6 个图

我做过的一个指标得分，指标数量有30个，主成分取了12个，最终结果没有太大变化
我做过的一个指标得分，指标数量有30个，主成分取了12个，最终结果没有太大变化

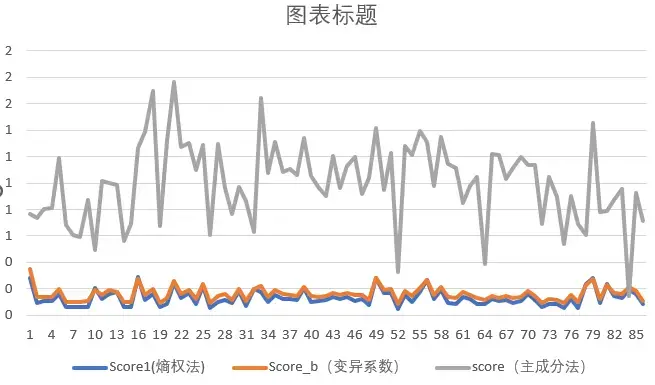
我做过的一个指标得分，指标数量有 30 个，主成分取了 12 个，最终结果没有太大变化

六、写作！！公式是否需要展示？

指数合成（尤其是数字经济、韧性……）、倾向匹配、东西南北异质性、DID、中介效应，如今已经成为泛滥的八股文。不少人把指数合成视为弄虚作假。喜欢用这种指标合成的一般也是横向课题（政府企业报告）非经济研究。最重要的是，大部分文章并不会贴出详细变化公式，这也是指数合成被诟病的原因——没说明的灰色地带太多。

个人建议是：不用写出公式，但要写明公式专属名词和细节操作，例如“有没有使用正负指标”，“是在使用极差法归一化后再统一使用的熵权法”“一级指标和二级指标之间有没有复用赋权法重新整合赋权”……

虽然这些方法已经被滥用、被质疑，但比起一知半解套用代码，了解他们的使用背景，结合选题详细地说明，或许这才是最重要的。

  1. 赵涛, 张智, 梁上坤. 数字经济、创业活跃度与高质量发展——来自中国城市的经验证据

    $$J$$

    . 管理世界,2020,36 （10）: 65-76. DOI: 10.19744/j.cnki. 11-1235/f.2020.0154. ↩︎

  2. Shannon, C. E. （2001）. A mathematical theory of communication. ACM SIGMOBILE mobile computing and communications review, 5 （1）, 3-55. ↩︎

  3. https://en.wikipedia.org/wiki/Entropy_(information_theory) ↩︎

  4. https://mp.weixin.qq.com/s/H-wFZOxWPUdwJBkpASu8bw ↩︎

收录于 合集・Stata 实证工具 9
更新于 2023-11-20 
CC BY-NC 4.0
阅读原始文档
LINE
Stata
返回 主页
切换 选择 ESC 关闭
搜索引擎 Fuse.js