计量经济学:Log (y+1) 的转化是否可靠

Log (y+1) 的转化是否可靠
摘要
| 标题: Logs with Zeros? Some Problems and Solutions |
|---|
| 作者: Jiafeng Chen; Jonathan Roth |
| 期刊: The Quarterly Journal of Economics (2024/3/30) |
| DOI: 10.1093/qje/qjad054 |
| 摘要翻译: 当研究一个结果变量 Y 可以等于 0 时 (例如收益) 时,多数研究者在估计时通常采用进行转换的平均处理效应 (ATE),这种转换在结果变量 Y 很大时,可以表现为 log (Y),定义为零值时,通常采用 log (1 + Y) 进行处理。我们的研究发现,此类对数转换的平均处理效应不应被解释为百分比效应,因为结果本身与百分比不同,平均处理效应的估计值取决于结果变量的单位。事实上,我们的研究表明,如果在进行类对数变换之前,改变 Y 的实际单位,就可以得到任意大小的处理效应。这种结果产生的原因是,对于在估计时结果从零变为非零的样本,样本水平的百分比效应没有明确定义,并且结果的单位隐含地决定了对数转换的平均处理效应在广延边际上的赋予权重。进一步研究中,我们发现了一个“不可能三角”: 当结果变量可以等于零时,不能同时满足估计结果即是样本的平均处理效应,且 Y 的单位不发生改变(或者说与单位变动无关)以及实现点识别。我们讨论了几种可能在具有集约边际和广泛边际的设置中是合理可行的替代方法,包括(1)以百分比表示平均处理效应水平 (例如使用泊松回归),(2) 明确校准置于集约边际与广泛边际上的样本,以及 (3) 分别估计广延边际和集约边际的实际处理效应 (例如使用 Lee bounds)。我们在三个实证应用中说明了这些方法。 |
省流的概括
讨论 包含 0 值的对数化 方式,例如 $log(1+y)$ 、$arcsinh(y)=\sqrt{1+y^2}+y$ 是否可靠。
代码例子
代码结果说明,数据中含有 0 时,可以通过对数化的 $y$ 单位修改影响回归显著性。
|
|
解释
认识对数化处理
一般认为对数化处理后的经济意义变动 百分比。
对变量取对数后,一般认为系数结果反映的是百分比变化。例如 lnGDP ,在回归中代表的 GDP 变化百分之几。如果是 reg lny lnx, 系数经济含义则是弹性。参见取对数的意义。
对于以下回归式子 $$ \ln y_n=\alpha+\beta x_n +\varepsilon $$ 其系数有如下经济含义 $$ \begin{align} \beta & = \frac{\ln Y_{n+1}-\ln Y_{n}}{X_{n+1}-X_{n}}\\ &=\frac{\ln \frac{Y_{n+1}}{Y_{n}}}{X_{n+1}-X_{n}}= \frac{\ln (1+\frac{Y_{n+1}-Y_{n}}{Y_{n}})}{\Delta X}\\ &= \frac{\ln (1+\Delta Y \% )}{\Delta X} \approx\frac{\Delta Y \% }{\Delta X} \end{align} $$ 有时研究者进行对数化还因为数据呈现长尾分布,对数化使得数据更加紧凑。
对数化的局限
文章核心结论是,当数据包含 0,且放缩单位有变化时(例如劳动经济学中经常使用每小时工资,每月工资,每周工资, 这涉及单位转化),对数化的估计会发生改变,因此不太可靠。
一般认为对数化后求出来的处理效应是一种百分比,和放缩参数 $\alpha$ 无关。 $$ \small ATE=E[\log(1+aY(1))-\log(1+aY(0))]=E\left[\log\left(\frac{1+aY(1)}{1+aY(0)}\right)\right] $$
进一步考虑数据结构,会产生变化 $$ \begin{aligned} \lim_{a\to\infty}\log\left(\frac{1+aY(1)}{1+aY(0)}\right)=\begin{cases}\log\left(\frac{Y(1)}{Y(0)}\right)&\text{if }Y(1)>0,Y(0)>0\\ 0&\text{if }Y(1)=0,Y(0)=0\\ \infty&\text{if }Y(1)>0,Y(0)=0\\ -\infty&\text{if }Y(1)=0,Y(0)>0 \end{cases} \end{aligned} $$ 上式的后三者说明了处理效应的估计值可能会受到影响。
文章关于对数化的偏差类似于 局部平均处理效应(LATE) 。
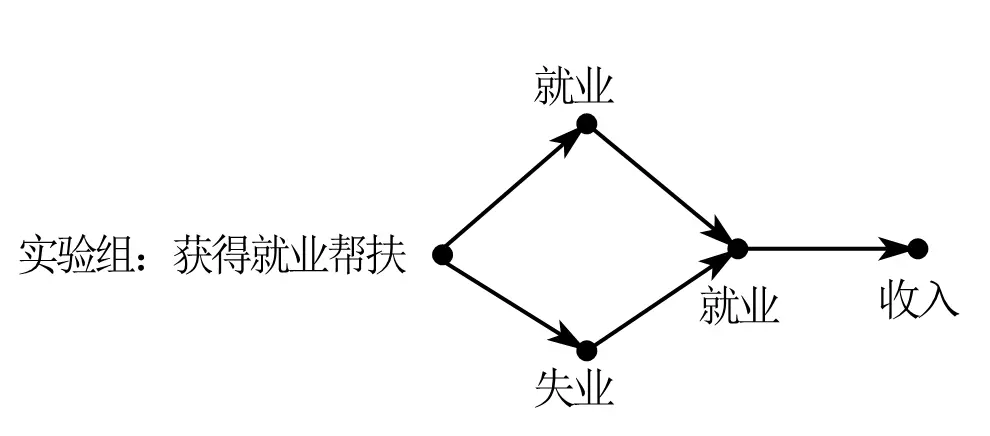
以就业政策为对象,政策冲击为实验组带来了不一样的反应 。
0 表示失业状态,1 表示就业状态。
原本实验组有失业人群 0 有就业人群 1,但是在政策冲击后全部变成了就业人群 1。
- 原本状态为就业 1,冲击后依旧为就业 1,但收入依旧有上升,此时解释变量的变化由政策冲击直接带来,为 集约边际(intensive margin)
- 原本状态为 0,冲击后变成了 1 ,解释变量变化除了政策冲击,还有自身状态改变带来的变化,这种变化为 广延边际(extensive margin)
于是处理效应的测度变成了以下情况:
因此平均处理效应也是两种边际效应的数学期望加总
$$ ATT=E(ATT^{int})+E(ATT^{ext}) $$
假如使用 $lg(1+x)$ 来变化,同时放缩单位,从千元变为元
对于 集约边际(intensive margin) 来说, $$ \begin{aligned} ATT_{1000}^{int}& =E{log(1000Y^{int}(1))-log(1000Y^{int}(0))} \\ &=E{log(1000)+logY^{int}(1))-log(1000)-logY^{int}(0))} \\ &=E{log(Y^{int}(1))-log(Y^{int}(0))}=ATT^{int} \end{aligned} $$ 对于 广延边际(extensive margin) 来说,
这部分是状态从 0 到 1 的部分,采用 $ln(y+1)$ d 对数化后,原本为 0 的部分依旧为 0。
$$ \begin{aligned} ATT_{1000}^{ext} & =E{log(1000Y^{ext}(1))-log(1000Y^{ext}(0))} \\ &=E{log(1000)+logY^{ext}(1))-0} \\ &=ATT^{ext}+\color{red}{log(1000)} \end{aligned} $$
总体处理效应是这以上两部分的数学期望加总 $$ \begin{align} ATT&=P \times ATT^{ext}+(1-P)\times ATT^{int}\\ &=ATT+\color{blue}{P\times log(a)} \end{align} $$ 其中 $\color{blue}{P\times log(a)}$ 就是改变回归结果的偏差部分。
正是因为有这种偏差,很多文章会把 0 值处理作为稳健性检验的一部分。
还有其他更复杂的情况讨论,不过个人就无法理解了。
结论和解决方法
结论
在面对包含 0 的解释变量样本时!
很多营销号夸大了文章的结论,文章批评的是解释变量包含 0 的对数化情况,处理效应估计上实际上有个不可能三角形。
解决方法
以下每个方法就是在不可能三角形中进行取舍。
- 采用普遍的归一化和标准化去量纲,这样就没有单位影响
- 泊松回归最大似然估计
- 去除 0 值样本
- 理清样本分布,进一步分解集约边际和广延边际。
- 采用其他参数 lee bounds 之类的(这个没看明白怎么做)