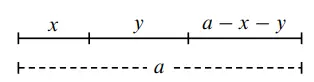用一根针测量π？概率论（茆诗松版) 笔记

这几天一直在看茆诗松版《概率论与数理统计》，本来看得是电子版，但看完后大呼过瘾，越看越觉得妙，于是连夜购入实体书。这本书确实如其在第一版前言中所讲的那样：例子生动有趣，同时把每个考点的狡猾变形娓娓道来，让人印象深刻。

特别感谢 github的re-book项目组 （2019）对书籍的 $\LaTeX$ 重排。

作为概率论与数理统计的入门书, 我们不想一进门就把学生引入数学天堂, 而是在“野外”先浏览概率统计的各种风景之后, 再进入数学天堂, 使各种概念和定理成为有源之水、有本之木。这样可使学生感到读此书的趣味, 感到与读数学教科书有不同的味道。当然我们也十分注意从偶然性中提炼出来的一些规律性的证明和论述，因为只有理解了的东西才能更深刻地感受它。

(第一版前言)

因为实在是太有趣，所以忍不住在知乎上重新记录下里面几个绝佳的例子。

一、用一根掉在地上的针估测π？

1、引入：几何概型

古典概型的基础笔记可以看我的另一篇回答：

古典概型的计算公式如下： $$ P(A)=\frac{事件A 所含样本点的个数}{\Omega中所有样本点的个数}=\frac{k}{n} $$ 几何概型则是把代数公式转化为面积（转换思想参见高中线性规划）： $$ P=\frac{S_{面积k}}{S_{面积n}} $$

几何概型举例

在长度为 a 的线段内任取两点将其分为三段, 求它们可以构成一个三角形的概率？

首线把线段分成三段, 长度分别为 $x,y,a-x-y$

围成三角形的充要条件为：任意两边之和大于第三边；任意两边之差小于第三边。

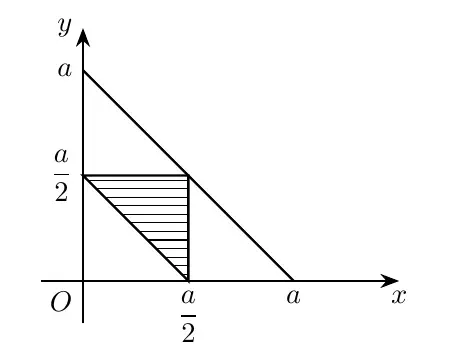
于是得到不等式限制： $$ \begin{cases} 0<a-x-y<x+y\\ 0<x<a-x-y\\ 0<y<x+(a-x-y) \end{cases} \stackrel{简化}{\longrightarrow} \begin{cases} \frac{a}{2}<x+y<a\\ 0<x<\frac{a}{2}\\ 0<y<\frac{a}{2} \end{cases} $$ 此时用 $x,y$ 建立坐标系看面积（线性规划那味儿）

$$ P=\frac{\frac{a^2}{8}}{\frac{a}{2}^2}=\frac{1}{4} $$

2、用一根针估计 $\pi$

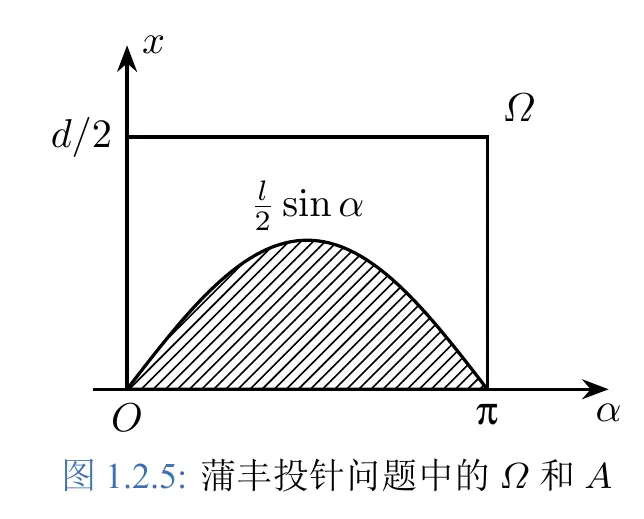
比丰投针问题（很著名，因为答案与 $\pi$有关）： 平面上画有间隔为 $d(d>0)$ 的等距平行线, 向平面任意投掷一枚长为 $l(l<d)$ 的针, 求针与任一平行线相交的概率？

如图，红色的就是那根针其与水平线夹角为 $\alpha$ 。

当针与平行线相交时，取针的中点向垂直方向投影，投影的垂线线段就被分成了两个部分。

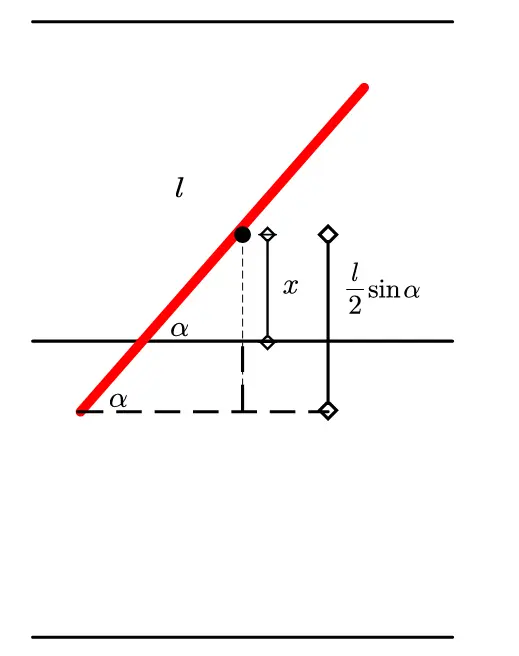
相交的充要条件变为：$x\leq\frac{1}{2}l \!sin\alpha$，此时未知参数就是 $x$ 和 $\alpha$ 。

同时得到参数的限制条件

$$ \begin{cases} 0 \le x \le d/2\\ 0 \le \alpha \le \pi \end{cases} $$ 通过两个参数建立坐标系。

然后通过微积分求得阴影部分的面积，除以矩形面积就是对对应概率。

$$ P (A) = \frac{S_A}{S_\Omega} = \frac{\int_0^\pi \frac{l}{2} \!sin \alpha , \mathrm{d} \alpha}{\frac{d}{2} \pi} = \frac{2l}{d\pi}\\ $$ 当 $2l=d$ 时，$P (A) =\frac{1}{\pi}$。

因此就可以通过越来越多次实验，然后相除，从而估测 $\pi$。

3、补充：如何确定概率

所谓的 “蒙洛卡特模拟” 就是在计算机中设计抽样模型，输入输出许多个随机值，通过最后的频率去逼近概率。

在茆诗松版教材中，专门花了一个小节讨论确定概率的方法

• 频率统计逼近概率
• 古典方法（排列组合、加法乘法原理….）
• 几何方法
• 主观方法（例如看起来明天下雨和不下雨的概率按理说是 50%平分，但是天气预报会说有 85%的概率下雨；还比如自己说有六成把握做成某件事…. 如此种种就是主观概率）

二、问卷敏感问题的真实情况估计

设计问卷的难点之一就是有些问题别人不愿意回答，或者不给出正确答案。

例如“夫妻间吵架频率”、“你是否浏览过不良网站”、“你家的收入是多少”… 由于“回答有损尊严”或者"不真实的回答"有利于搭便车（认为降低收入回答会让自己收到更多政府的帮助），我们很难得到正确的答案。

茆诗松版概率论在讲解条件概率时给出一个例子，或许可以让答卷人的答案更有效。

（虽然受困于效率，估计是实行不了的，但在问卷设计中就使用条件概率，这个切入点让人印象深刻）

1、引入：条件概率

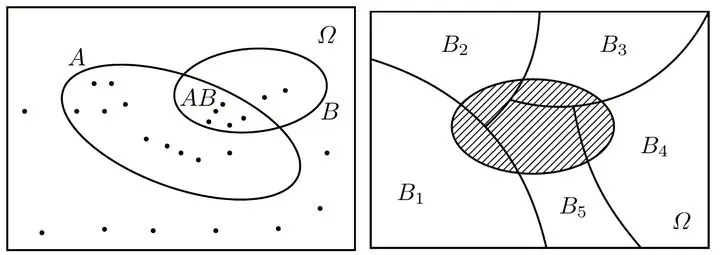
$$ P(A|B)=\frac{P(AB)}{P(B)}\stackrel{乘法公式}{\longrightarrow} P(AB) = P(B) P(A|B)\\ $$

$$ 全概率公式： P(A) = \sum_{i=1}^n P(B_i) P(A | B_i)\\ $$

$$ 贝叶斯公式： P (B_i | A) = \frac{P(B_i) P(A|B_i)}{\sum_{j=1}^n P(B_j) P(A|B_j)} \newline $$

$$ i = 12,\dotsc,n $$

条件概率的三公式中：

• 乘法公式是求事件交的概率。
• 全概率公式是求一个复杂事件的概率。
• 贝叶斯公式是求一个条件概率。

2、如何操作

调查者只需要回答以下两个问题中的一个就行，且选项只有“是”和“否”

• 问题 A: 你的生日是否在 7 月 1 日以前？
• 问题 B：你是否浏览过不良网站？

（1）被调查者在封闭屋子中没有其他观测者，独自一人操作和回答问题。

（2）调查者抽取盲盒，抽到红球回答 A, 抽到白球回答 B。

首先，我们能大致估测“任选一人，生日是否在 7 月 1 日以前”的概率，我们假定为 0.5。

此时，有 $n$ 个问卷，我们得到了 $k$ 份问卷选“是”，盲盒中抽到红球的概率为$ \pi$ 。

也就是说，我们有四个数据（$n，k，\pi，0,5$ ）。

此时，利用全概率公式：

$$ P(是)P(白球）P(是|白球)+P(红球）P(是|红球) \stackrel{带入数值}{\longrightarrow} $$

$$ \frac{k}{n}=0.5(1-\pi)+{p_{是|红球}}\pi \stackrel{解得}{\longrightarrow} $$

$$ {p_{是|红球}}=\frac{\frac{n}{k}-0.5(1-\pi)}{\pi} $$

心理学、统计学的交叉设计！一场精美的骗局到此结束！

三、“狼来了”的寓言与贝叶斯公式

1、引入：贝叶斯公式

贝叶斯公式： $$ 贝叶斯公式： P (B_i | A) = \frac{P(B_i) P(A|B_i)}{\sum_{j=1}^n P(B_j) P(A|B_j)}
$$

$$ i = 1,2,\dotsc,n $$

在贝叶斯公式中, 如果称 $ P (B_i)$ 为 $B_i$ 的 先验概率 ,称为$P (B_i |A) $ 为 $B_i$ 的 后验概率 , 则贝叶斯公式是专门用于计算后验概率的, 也就是通过 $A$ 的发生这个新信息, 来对 $B_i$ 的概率作出的修正。

例如在“狼来了”的故事中，村民对小男孩的有个初始信任度，但在小男孩反复的欺骗下，信任度不断降低，导致后面说真话也不相信小男孩了。

2、狼来了的寓言

记事件 $A$ 为“小孩说谎”，记事件 $B$ 为“小孩可信”。

假设村民最开始对小孩的印象是 $P(B)=0.8$ , $P(\overline{B})=0.2$。

先带入村民视角的条件概率，同时假设初始值

$$ \begin{cases} 小孩可信的同时说谎：P(A|B)=0.1\\ 小孩不可信的同时说谎：P(A|\overline{B})=0.5 \end{cases}\ $$ 当小孩说谎后，村民会重新评估对小孩的信任度，所以此时前提是小孩撒过谎，信任表示为 $P(B|A)$。

在第一次说谎后，带入贝叶斯方程：

$$ \begin{align*}
P(B|A) & = \frac{P(B)P(A|B)}{P(B)P(A|B) + P(\bar B)P(A|\bar B) } \\
& = \frac{0.8\times0.1}{0.8\times0.1 + 0.2\times0.5} = 0.444 \end{align*} $$ 也就是说村民对小孩信任变化如下：

$$ 先验概率 \begin{cases} P(B)=0.8\\ P(\overline{B})=0.2 \end{cases} \stackrel{欺骗一次}{\longrightarrow}后验概率 \begin{cases} P(B|A)=0.444\\ P(\overline{B}|A)=0.556 \end{cases} $$ 也就是说，欺骗一次后，村民对小孩的信任概率变为 $P({B})=0.444$ 和 $P({B})=0.556$。

同理反复带入，当欺骗第二次后，信任变为

$$ P(B|A) = \frac{0.444\times0.1}{0.444\times0.1 + 0.556\times0.5} = 0.138 $$ 综上，在两次欺骗后，村民对小孩的信任从 $P(B)=0.8$ 变为了 $P(B)=0.138$ 。

这就是多次欺骗导致了丢失信任。