收敛:从“算式的极限”到“增长的极限”

在经济学课程中,大部分概念往往会经历“数学含义-经济含义-统计含义”三次重新理解。我们总是在不同的地方见到同一个东西,但是却很少一口气把它通拉理解一遍,例如三个计算式。
本文将概括下“收敛”这个概念在三个环节的贯穿(虽然关联性似乎不强,但我还是想梳理一遍)
一、高数: 极限和收敛
极限和收敛,一开始就是一回事儿。
主要参考同济版《高等数学》1,收敛是作为极限的一种描述状态引入:
数列的极限中(上册 21 页),数列 $x_n$ 收敛于 $a$ ,记为 $\lim_{n \rightarrow \infty}{x_n=a}$。
函数的极限中(上册 33 页),函数收敛,记为 $\small \lim_{n \rightarrow \infty}{f(x_n)}=\lim_{n \rightarrow x_0}{f(x)}$ 。
级数的极限中(下册 252 页),$\small s=u_1+u_2+u_3+…u_i+…$ 无穷级数收 $u_i$ 敛,意味着 $\small \lim_{n \rightarrow \infty}{s_n=s}$ 反之则为发散。 $$ 收敛分类 \begin{cases} 内容 \begin{cases} 绝对收敛\newline 条件收敛 \end{cases}\newline 形式\begin{cases} 逐点收敛\newline 一致收敛 \end{cases} \end{cases} $$ 其中,级数收敛又分为绝对收敛和条件收敛; 逐点收敛和一致收敛
绝对收敛: $\small \sum_{n=1}^{\infty}{|u_n|}$ 收敛,则称 $\small \sum_{n=1}^{\infty}{u_n}$ 绝对收敛。
条件收敛:$\small \sum_{n=1}^{\infty}{|u_n|}$ 不收敛,$\sum_{n=1}^{\infty}{u_n}$ 收敛,则称 $\small \sum_{n=1}^{\infty}{u_n}$ 条件收敛。
点点收敛: $\small \exists{0<x<\delta},\forall\varepsilon>0, |f(x)-A|<\varepsilon$,$\small \exists{0<x<\delta},\forall\varepsilon>0, |f(x)-A|<\varepsilon$
一致收敛: $\small \exists{0<|x_1-x_2|<\delta},\forall\varepsilon>0,|f(x_1)-f(x_2)|<\varepsilon$,$\small \exists{0<|x_1-x_2|<\delta},\forall\varepsilon>0,|f(x_1)-f(x_2)|<\varepsilon$
顺便提一手收敛半径,也就是能让级数 $\small u_n(x)$ 收敛的 $x$ 的范围值。
收敛发散判定答题有没有捷径呢? 我的高数老师就说了一个“幽默”的方法,我在知乎上还刷到过:
你看这两个字,是不是既收敛又发散(
二、概率论:大数定理与中心极限
你以为的“偶然”往往蕴含在“必然”之中。有人必然中彩票,只是那个人偶然是你。
参考茆诗松版《概率论与数理统计》2,随机变量序列有两种收敛方式,依概率收敛和依条件收敛。
依概率收敛:$\bbox[#def,5px,border: 1px solid]{ x\stackrel{P}{\longrightarrow}c }$
例如丢硬币,可能一开始正面朝上的几率偏离 $\frac{1}{2}$ 的幅度极大,当投掷的次数越来越多后,频率就会趋近于概率。频率统计成了确定概率3的方法之一。
各种版本的大数定理大数定理 $\boxed{ 大数定理 }$ 基本说的都是一件事:随着实验次数 n 的增加,概率与频率的偏差值 $\small \frac{S_n}{n}-P$ 大于预先给定的一个值 $\varepsilon$ 的可能性会越来越小。
无论是伯努利(Bernolli)大数定理、切比雪夫大数(chebyshev)定理、马尔科夫(Markov)大数定理、辛钦(Khinchin)大数定理,本质上说的都是这一件事4。
依分布收敛:$\bbox[#def,5px,border: 1px solid]{ x\stackrel{F}{\longrightarrow}c }$
强分布收敛是点点分布收敛,弱分布收敛是去掉间断点只考虑 $F(x)$ 的连续分布。
表示为$ \mathbb{P}(X_n\leqslant a)\to\mathbb{P}(X\leqslant a) $也就是$ \lim_{n\to\infty}F_n (x)=F (x)$ 。
$\boxed{ 中心极限定理 }$ 说的是这样一件事:一定条件5下,独立随机变量和的 $Y_n=\sum_{n}^{i=1}{X_i}$ 分布函数会趋于正态分布。
有趣的函数分布知识6
- 假设存在一个随机变量,满足二项分布。
- 当它趋于极限,期望等于方差,就成了泊松分布。
- 随机变量间的间隔则满足指数分布。
- 第 n 次变量对应的横坐标服从伽马分布。
三、经济学意义:收敛效应
货币≠数字,运营≠算题,经济≠数学
1、收敛假说(趋同)
来自“区域经济学”课老师用过的资料 《高级经济地理学》 (贺灿飞著)。
随着索罗(solow)模型的提出, 发展经济学研究者们发出了疑问:
既然,每个经济体有自己的稳态点与平衡增长路径。
同时,落后的经济体发展地很快,先进的经济体发展的速度不断减缓。
那么问题来了,最后大家的经济增长会不会趋同呢? $$ \begin{cases} \beta收敛 \begin{cases} 绝对收敛\newline 条件收敛\newline 俱乐部收敛 \end{cases}\newline \sigma收敛 \end{cases} $$ $\beta$ 收敛:
- $\boxed{\beta 绝对收敛}$ 认为:无论经济体初始情况如何,由于弱者发展快,强者发展慢,最后经济发展总是收敛到一致的水平。我们需要的只是“一点点”耐心。
- $\boxed{\beta 条件收敛}$ 认为:经济体的增长速度受某些环境结构(例如人口结构,要素禀赋,要素增长率)影响,因此不同的经济体收敛于不同的稳态,最后发展的结果也不同。
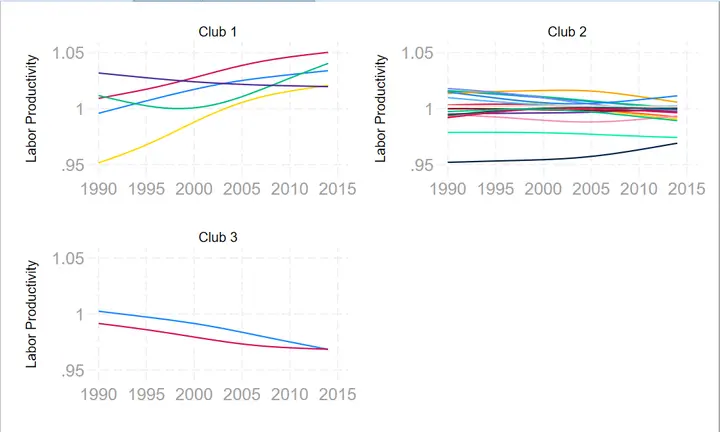
- $\boxed{俱乐部收敛}$ 认为:初期经济发展水平接近的经济集团和较富的国家集团各自内部存在条件收敛,而两个集团之间却没有收敛的迹象。
$\sigma$ 收敛:
- $\boxed{\sigma收敛}$ 认为:不同经济体间的标准差 $\sigma$ 总是在不断缩小。
2、收敛速度
似乎是实分析中的数学概念,但我第一次学是在**Romer**的《高级宏观经济学》中学到的,所以归纳到经济部分。
查了下维基百科(Rate of convergence),主要应用在算法优化和深度学习领域。
若序列 $x_k$ 收敛于 $L$,下式 $\mu$ 就是收敛率的表达式。
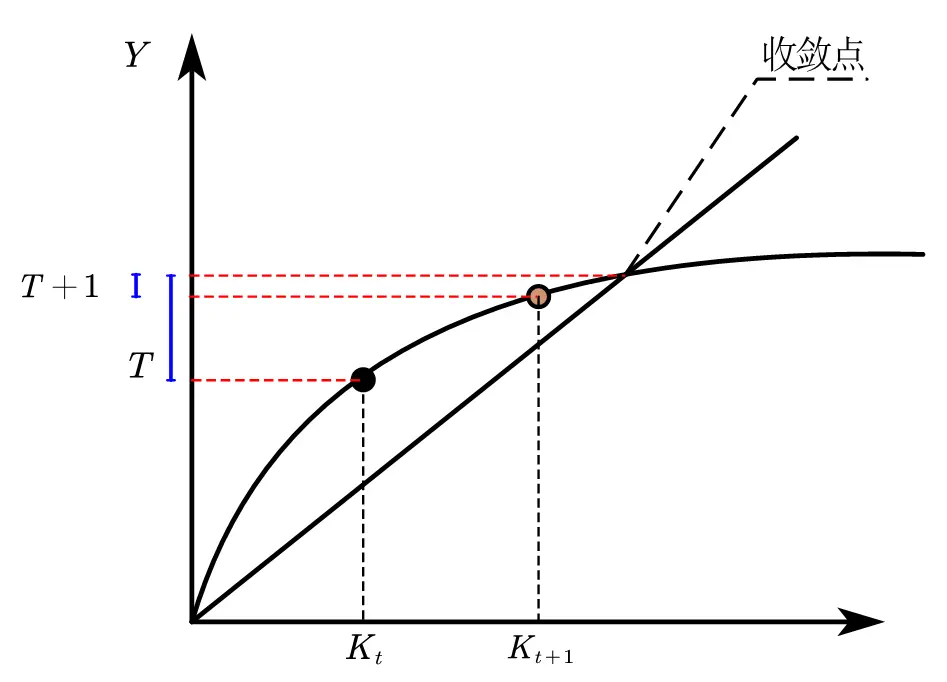
$$ \lim_{k\to\infty}\frac{|x_{k+1}-L|}{|x_k-L|^q}=\mu $$ 当式子中的 $q=1$ 时,就是线性收敛收敛速度就是 $t$ 和 $t+1$ 时刻,数值到收敛点的数值差距之比。
想象下跑步比赛。我们衡量快慢,比较的是从起点开始的距离。
收敛则像我们在焦急的等待下课铃。我们在意的是距离多久才能到终点。
如何表示 $T$ 时刻和 $T+1$ 时刻呢?经济分析中通常使用泰勒展开近似。
以 solow 模型为例,$\dot{k}=sf(k)-(n+g+\delta)k$,所以动态分析上, $\dot{k}$ 为 $k$ 的函数,我们写作 $\dot{k}(k)$ 。
稳态点时,$k=k^*$,$\dot{k}=0$
在 $k=k^*$ 时,对 $\dot{k}(k)$ 作一阶泰勒展开近似
$$ \dot{k}\simeq[\frac{\partial\dot{k}(k)}{\partial k}|_{k=k^{*}}](k-k^{*})=-\lambda[k(t)-k^{*}] $$
$$ \begin{aligned} &\lambda\equiv-\frac{\partial\dot{k}(k)}{\partial k}\Bigg|_{k=k^{*}}\newline & =-\left[sf^{\prime}(k^{*})-(n+g+\delta)\right] \newline &=(n+g+\delta)-sf^{\prime}(k^{*}) \newline &=(n+g+\delta)-\frac{(n+g+\delta)k^{*}f^{\prime}(k^{*})}{f(k^{*})} \newline &=[1-\alpha_{k}(k^{*})](n+g+\delta)\newline \end{aligned} $$
$\lambda$就是我们要找的收敛速度
四、计量统计7
1、计量方程
(1)绝对趋同
Barro 和 Martin(1991)8在 Baumol(1986)9的基础上提出了绝对 $\beta$ 趋同的检验方程。
$$ \small \frac1T\left[\log(y_{i,t+T})-\log(y_{i,t})\right]=\alpha-\frac{(1-\mathrm{e}^{-\beta T})}T\log(y_{i,t})+\varepsilon_i $$ 其中 $i$ 表示 $i$ 个地区, t 表示期初,$ t+T $表示期末,$ T $表示观测时期长度,$ y_i $,$ t $表示地区$ i$在 $t$ 期的人均 GDP,$\beta$ 表示趋同速度。如果 $\beta>0$ ,则说明不同地区经济发展的差异会逐渐消除,最终达到同样的稳态。
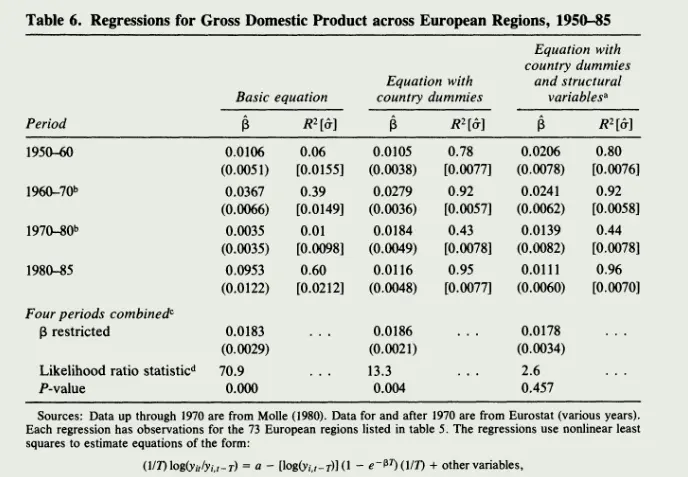
上面的公式是根据新古典经济增长模型推导而来(也就是 solow model)。
个人觉得国内关于收敛回归方差的描述清晰简洁不少。这里参考彭国华(2005)10的回归式子: $$ g=c+\beta{\ln y_0}+\varepsilon $$ $g$ 就是增长率, $c$ 是常数项,$y_0$ 是真实产出,$\varepsilon$ 是误差项。当 $\beta<0$,也就说明了增长率 $g$ 和经济水平 $y_0$ 负相关。符合我们“高水平经济体增速较慢,低水平经济体增速较高”的假设。
(2) 条件趋同
Barro 和 Martin (1992)11在绝对 $\beta$ 趋同检验方程的基础上又提出了条件 $\beta$ 趋同的检验方程:
$$ \small \frac{1}{T}\left[\log(y_{i,t+T})-\log(y_{i,t})\right]=\alpha-\frac{(1-\mathrm{e}^{-\beta T})}{T}\log(y_{i,t})+\lambda X_{i,t}+\varepsilon_{i,t} $$ 结论和参数含义和绝对趋同一样,因为条件趋同的含义是经济增长与经济体环境结构相关,所以多了 $X_{i,t}$ 作为控制变量。
引入控制变量 $X_{i,t}$ 麻烦的点在于又得去研究外生性了,,,,,,
(3) 俱乐部趋同
具有相同的经济特征、具有类似增长路径的集团内部存在趋同,在不同的经济集团之间则不存在趋同,这种现象称为俱乐部趋同(Durlauf,1995; Galor,1996)。 $$ \frac1T\left[\log(y_{i,t+T})-\log(y_{i,t})\right]=\alpha+\beta\mathrm{log}(y_{i,t})+\lambda D+\varepsilon_{i,t} $$ 变量含义与上面相同,不同的是当 $\beta<0$ 才说明趋同, $D_{i,t}$ 是虚拟变量,也就是分组,例如整个东亚可能是同样的发展路径,或者某几个城市都是作为港口城市进行发展。
发现的比较有趣的研究是以什么标准聚类分类俱乐部,比如以“中等收入陷阱”为聚类分类标准建模12。
Du (2017) (这位居然是山东大学的)引入了 Stata 包来执行 Phillips 和 Sul (2007) 的计量经济学收敛分析和俱乐部聚类算法。
分组依据思想大概如下
$$ \lim_{ x\rightarrow +\infty}{\frac{X_j}{X_i}}\rightarrow1 $$ 想详细看数学推导1314的可以点击他们的名字的超链接看。
关于俱乐部聚类的 stata 操作,youtube、GitHub 有很好的教程。
我把他的 do 文件进行了部分翻译和细节补充:
注意使用 cd 调整 stata 的工作读取环境(已写进 do 文件的注释)
|
|
2、实证结果(例子)
中国目前的实证结果基本就是满足 $\sigma$ 收敛15和俱乐部收敛(分类一般是中东西部这种区域分类)16。GDP、全要素、工业产出作为标准基本是一样的结论17。
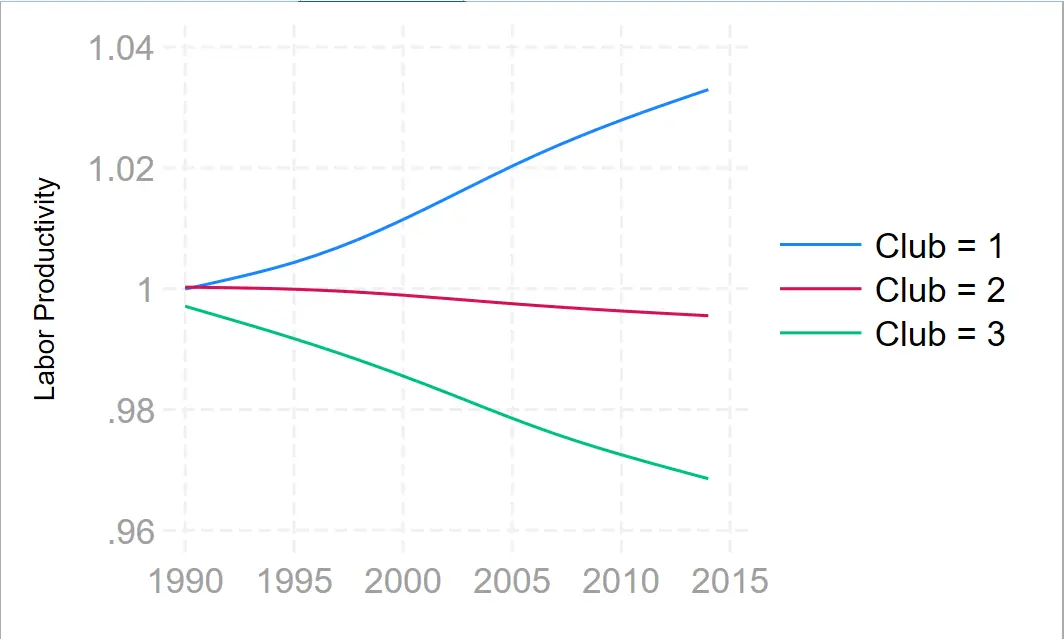
-
个人觉得同济版教材的微积分部分还是很不错的,但是绝对别用其线代部分。定义方面,同济版定义的方向导数和有些数学分析教材并不相同。 ↩︎
-
个人觉得国内最好的统计学教材,尤其是在概率论部分,引人入胜。数理统计那部分相对学起来无趣一些 ↩︎
-
其他还有几何法、主观法、代数法 ↩︎
-
真要各自解释这几个大数定理,我自己反正是记不清 ↩︎
-
具体是啥条件我已经忘记,机器学习应用时,感觉满足挺难的 ↩︎
-
所以我说,经管版概率论教材就是不行,如果不看统计学教材,就错过了这么连贯的知识点理解。所以这些分布本身就是一步一步发展过来的。如果不知道这种发展,还以为是隔空投送呢 ↩︎
-
这部分主要参考了《区域与城市经济学》(踪家峰著) ↩︎
-
Barro R J, Sala-i-Martin X, Blanchard O J, et al. Convergence across states and regions[J]. Brookings papers on economic activity, 1991: 107-182. ↩︎
-
Baumol, W. J. (1986). Productivity Growth, Convergence, and Welfare: What the Long-Run Data Show. The American Economic Review, 76 (5), 1072–1085. http://www.jstor.org/stable/1816469 ↩︎
-
彭国华. 中国地区收入差距、全要素生产率及其收敛分析[J]. 经济研究, 2005 (9): 11. DOI:CNKI:SUN: JJYJ. 0.2005-09-003. ↩︎
-
Barro R J, Mankiw N G, Sala-i-Martin X. Capital mobility in neoclassical models of growth[R]. National Bureau of Economic Research, 1992. ↩︎
-
徐永慧, 李月, 邓宏图. 俱乐部收敛与中等收入陷阱[J]. 现代财经 (天津财经大学学报), 2022,42 (11): 48-62. DOI: 10.19559/j.cnki. 12-1387.2022.11.004. ↩︎
-
Du, K. (2017). Econometric convergence test and club clustering using Stata. The Stata Journal, 17 (4), 882-900. ↩︎
-
Phillips, P. C., & Sul, D. (2007). Transition modeling and econometric convergence tests. Econometrica, 75 (6), 1771-1855. ↩︎
-
林毅夫, 刘明兴. 中国的经济增长收敛与收入分配[J]. 世界经济,2003 (08): 3-14+80. ↩︎
-
沈坤荣, 马俊. 中国经济增长的“俱乐部收敛”特征及其成因研究[J]. 经济研究,2002 (01): 33-39+94-95. ↩︎
-
汤学兵, 陈秀山. 我国八大区域的经济收敛性及其影响因素分析[J]. 中国人民大学学报,2007 (01): 106-113. ↩︎