书接上回，本文是《An Introductory Guide to Event Study Models》的代码学习记录。
附录 A：区分 DID 和 Timing-base
这部分代码属于描述统计，描述样本分布（或者作为政策实施背景）。
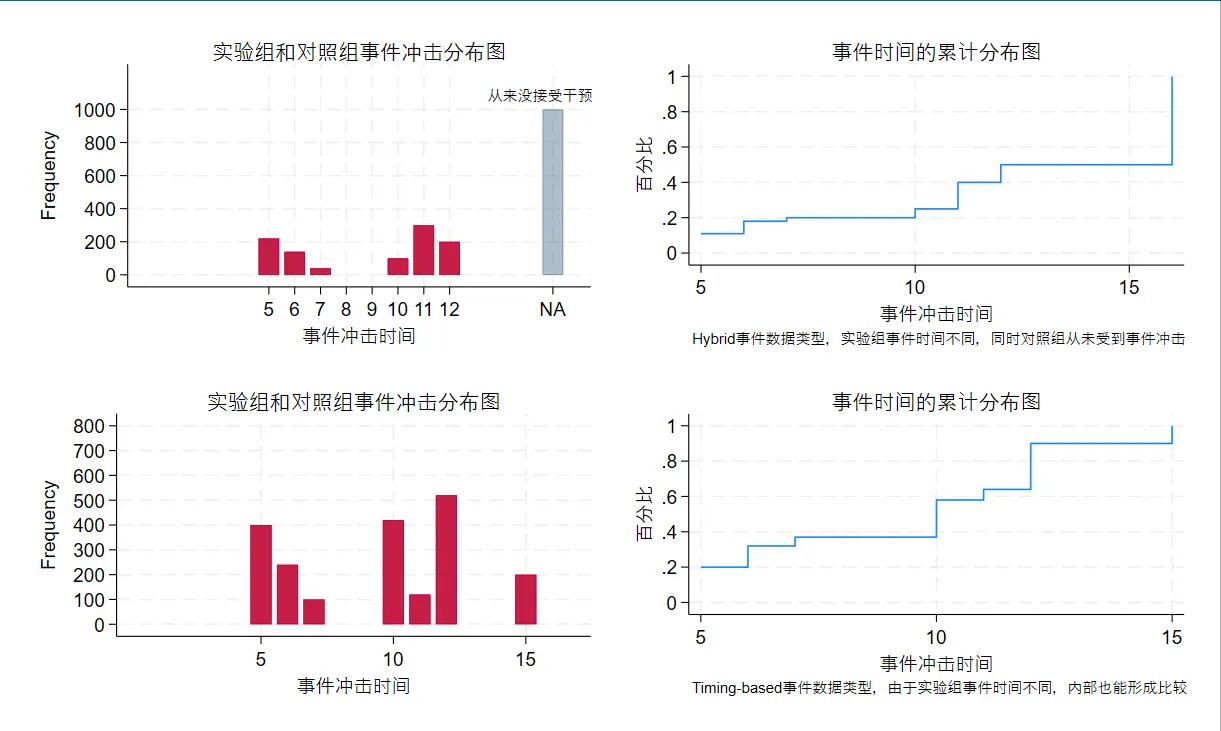
- DID type：既有实验组又有对照组（从未实施过政策）
- Timing-based：只有实验组，但实验组内部事件冲击时间不同。
代码结果：第一排Hybrid数据结构；第二排Timing-based数据结构
代码如下，结构是生成数据-画频率图-画累计图。原文累计图先使用 cumul 计算积累比例值，然后通过 twoway 画折线图。太复杂了，这里修改成 cdfplot 命令一步到位。
结果图片和原文不同也不用意外——原文代码在两侧额外插值插入了端点值，我删去了这部分。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
|
clear
*-生成双重差分面板随机数据
set seed 2024
set obs 100
gen i = _n
gen treated = i > 50
gen E_i = 11 if treated == 1
expand 20
sort i
qui by i: gen t = _n
xtset i t
*-设置处理效应
gen D = (t == E_i)
gen etime = (t - E_i)
label var i "个体编号"
label var t "日期"
label var D "did变量=time*post"
label var E_i "事件冲击时间"
*-画出实验组和处理组的分布
replace E_i=16 if treated==0
replace E_i=5 if treated==1 & i>=51 & i<=61
replace E_i=6 if treated==1 & i>=62 & i<=68
replace E_i=7 if treated==1 & i>=69 & i<=70
replace E_i=10 if treated==1 & i>=71 & i<=75
replace E_i=11 if treated==1 & i>=76 & i<=90
replace E_i=12 if treated==1 & i>=91
#delimit ;
/*
分界符设置，修改分号；为命令分行符号。
如此以来，除非末尾加上分号，即便分行写也看作一排
画图命令这样使用会方面很多
*/
twoway (histogram E_i if treated==1, discrete frequency start(4) barwidth(0.8) xscale(range(0 17)) yscale(range(0 1200)) color(cranberry%100))
(histogram E_i if treated==0, discrete frequency start(4) barwidth(0.8) xscale(range(0 17)) yscale(range(0 1200)) color(navy%40)),
title("实验组和对照组事件冲击分布图",
color(black) size(v.small)) legend(off)
xlabel( 5 "5" 6 "6" 7 "7" 8 "8" 9 "9" 10 "10" 11 "11" 12 "12" 16 "NA")
text(1100 15.5 "从来没接受干预", size(small))
name(histogram4 , replace);
#delimit cr
*-画出实验组和处理组的分布
preserve //保存当前数据集
#delimit ;
cdfplot E_i,
title("事件时间的累计分布图",
color(black) size(v.small)) legend(off)
ytitle(百分比)
name(CDF4, replace)
note(Hybrid事件数据类型，实验组事件时间不同，同时对照组从未受到事件冲击)
;
#delimit cr
restore //重新加载保存数据集
*-实验组和处理组的分布
replace treated=1
replace E_i=5 if treated==1 & i>=1 & i<=20
replace E_i=6 if treated==1 & i>=21 & i<=32
replace E_i=7 if treated==1 & i>=33 & i<=37
replace E_i=10 if treated==1 & i>=38 & i<=58
replace E_i=11 if treated==1 & i>=59 & i<=64
replace E_i=12 if treated==1 & i>=65 & i<=90
replace E_i=15 if treated==1 & i>90
#delimit ;
twoway (histogram E_i if treated==1, discrete frequency start(4) barwidth(0.8) xscale(range(0 17)) yscale(range(0 800)) color(cranberry%100)),
title("实验组和对照组事件冲击分布图",
color(black) size(v.small)) legend(off)
ylabel(0(100)800)
name(histogram5 , replace)
;
#delimit cr
*-画出实验组和处理组的累计分布
#delimit ;
cdfplot E_i,
title("事件时间的累计分布图",
color(black) size(v.small)) legend(off)
ytitle(百分比)
note(Timing-based事件数据类型，由于实验组事件时间不同，内部也能形成比较)
name(CDF5, replace)
;
#delimit cr
*-合并展示以上图
graph combine histogram4 CDF4 histogram5 CDF5
iscale 0.25 //图片比例缩小为四分之一
|
附录 B：Timing-based 的参数限制
在估计 DID 的事件效应时，一般不加入时间趋势，但会加入个体固定和时间固定，这些固定效应的作用是分解截距。处理共线性的方法一般是默认 $t_{-1}$ 为 0 、合并删除部分变量、施加其他约束、非线性化……
对于 Timing-based 的数据形式，由于没有对照组，我们只能在实验组内部进行比较。需要的加入的参数限制会更多。
- 事件时间的差异也是提供信息的一部分。
- 实验组之间事件时间差异最小值越大，信息流失越多。
- 个体越多，信息越多。
于是附录 B 计量代码研究的是——
当研究 Timing-based 数据结构时，对于不同的时间分布和个体分布，需要多少个额外参数才能求解？
个人理解：这里可能是通过一系列回归建立方程组，通过方程组建立矩阵，再通过矩阵秩来判断，还需要多少个参数约束才能求解。
附录B代码结果：一张作者说非常奇怪的结果图
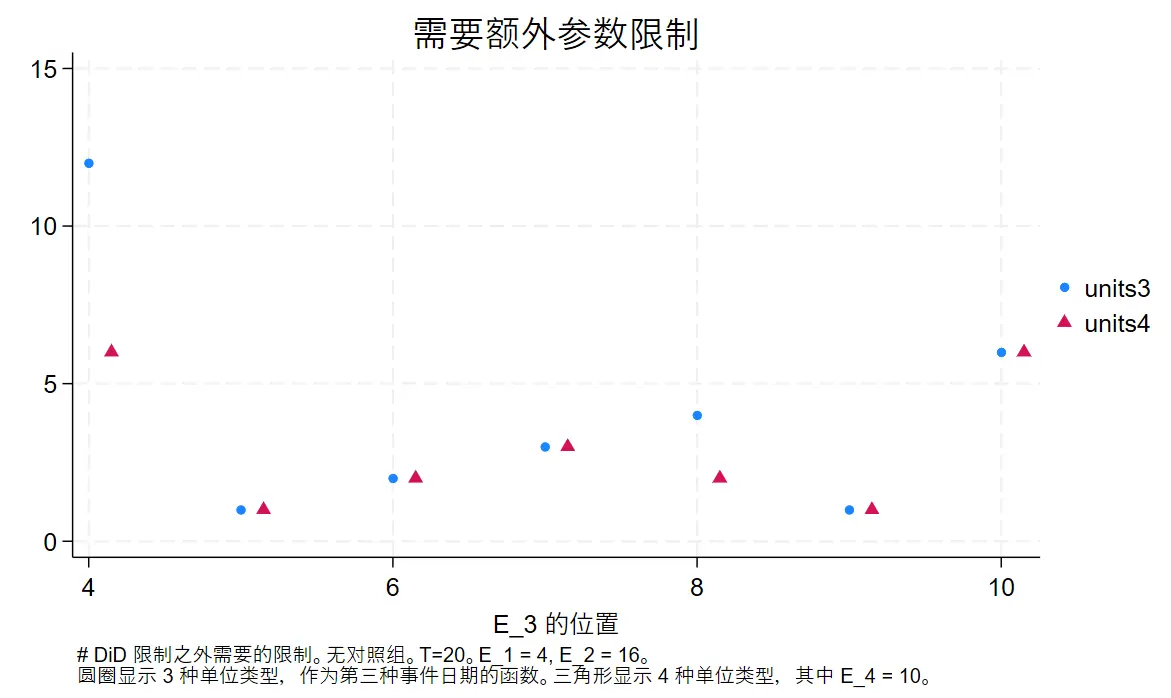
解释下附录 B 代码的结果图含义。
先给出一个数据集，都受到事件冲击，但事件时间不同。初始样本生成的数据集中，事件冲击时间分别是 4 和 16。此时求解需要的额外约束参数为 12（可以理解为自由度估计还差多少）。
图像的含义是：
先看蓝色圆点部分第一列。
当加入其他样本，且样本点事件冲击时间为 4 (横坐标)时，此时没有带来额外信息。整体数据集依旧是两类样本——事件冲击时间为 4 或 16，求解需要的额外参数依旧为 12(纵坐标)。
同理，蓝色圆点第二列的含义是，加入时间冲击时间为 5 的第三组样本，由于事件冲击时间差异减少，信息增多，此时需要的额外参数减少为 1。
红色三角形的含义则是在给定每列圆点数据的基础上，再加入三角形代表的样本，需要的参数又会发生什么变化。
本来预期，时间差异给定的情况下，个体分组越多，额外参数需求越小，没想到只有第五列出现了这种情况，所以论文情况说这很奇怪，也值得研究，但他也不知道为什么。
以下代码通过 GPT 加入注释：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
|
#delimit ;
cap log close ;
set trace off ;
set more off ;
clear all ;
set seed 101 ;
cap prog drop runme ;
prog def runme ;
args list ctrl trends ;
qui gendata "`list'" `ctrl' `trends' ;
qui forvalues i = 0/20 { ;
gen D_p`i' = (etime == `i') ; // 生成处理组正向虚拟变量
gen D_m`i' = (etime == -1 * `i') ; // 生成处理组负向虚拟变量
summ D_p`i' ; // 汇总处理组正向虚拟变量
local dropme = (r(mean) == 0) ;
if `dropme' == 1 { ;
drop D_p`i' ; // 如果均值为0，则删除处理组正向虚拟变量
} ;
summ D_m`i' ; // 汇总处理组负向虚拟变量
local dropme = (r(mean) == 0) ;
if `dropme' == 1 { ;
drop D_m`i' ; // 如果均值为0，则删除处理组负向虚拟变量
} ;
} ;
drop D_m0 ; // 删除处理组负向虚拟变量的基准情况
egen unittype = group(E_i) , miss ; // 根据 E_i 生成单位类型变量，处理缺失值
qui tab unittype , gen(udum) ; // 汇总单位类型变量，生成对应的虚拟变量
qui tab t , gen(tdum) ; // 汇总时间变量，生成对应的虚拟变量
unab vars : D_* udum* tdum* ; // 生成所有与 D_*、udum* 和 tdum* 相关的变量列表
mata: count() ; // 调用 Mata 函数计算变量的统计信息
local c1 = count[1,1] ; // 获取统计结果中的第一列信息
local c2 = count[1,2] ; // 获取统计结果中的第二列信息
local c3 = count[1,3] ; // 获取统计结果中的第三列信息
di "`list'" _column(20) `c1' _column(25) `c2'
_column(35) `c3' ; // 显示变量列表及其统计信息
end ;
mata: ;
void count()
{ ;
v = st_local("vars") ; // 获取 Stata 定义的局部宏变量 "vars"
X = st_data(.,v) ; // 从当前数据集中获取变量数据
mycols = cols(X) ; // 计算数据矩阵的列数
myrank = rank(X) ; // 计算数据矩阵每列的非缺失值数量
gap = mycols - myrank ; // 计算数据矩阵每列的缺失值数量
output = (mycols,myrank,gap) ; // 将统计结果组合成元组
st_matrix("count",output) ; // 将统计结果存储到名为 "count" 的矩阵中
} ;
end ;
cap prog drop gendata ;
program define gendata ;
args list ctrl trends ;
drop _all ;
local numobs = 48 ; // 定义观察值数量
local treatedunittypes = wordcount("`list'") ; // 计算处理单元类型数量
/* "ctrl" is 0/1 whether we have control (untreated) units */
/* if we have them, put half of data into control units */
local numtreatedobs = round(`numobs' / (1 + `ctrl')) ; // 计算处理单元观察值数量
local numuntreatedobs = `numobs' - `numtreatedobs' ; // 计算对照单元观察值数量
local obspertype = floor(`numtreatedobs' /
`treatedunittypes') ; // 计算每种处理单元类型的观察值数量
forvalues i = 1/`treatedunittypes' { ;
local eventdate_`i' = word("`list'",`i') ; // 获取每种处理单元类型的事件日期
} ;
set obs `numobs' ;/* 观察值数量 */
gen i = _n ;
gen treated = i > `numuntreatedobs' ;/* 处理组单元 */
gen E_i = . ;
forvalues i = 1/`treatedunittypes' { ;
local start = (`i'-1)*`obspertype' + `numuntreatedobs' + 1 ;
local stop = (`i')*`obspertype' + `numuntreatedobs' ;
replace E_i = `eventdate_`i'' if i >= `start' & i <= `stop' ; // 根据每种处理单元类型设置事件日期
} ;
replace E_i = `eventdate_`treatedunittypes'' if i > `stop' ;
tab E_i , miss ; // 汇总事件日期变量，显示缺失值情况
expand 20 ;/* 时间期限 */
sort i ;
qui by i: gen t = _n ;
xtset i t ; // 定义面板数据的单位和时间变量
/* make variables that determine the DGP */
gen etime = (t - E_i) ;/* 事件时间 */
/* gen TE = 1 * (etime >= 0) ;/* 步骤功能处理效应 */
*/
gen TE = (etime >= 0) * (etime+1) ;/* 无尽的斜坡功能处理效应 */
replace TE = 0 if E_i == . ;
gen Y0_pure = 0 ;/* 最简单的反事实情况 */
*gen Y0_pure = 4 * treated + 0.3 * treated * t ;/* 处理组有前趋势 ... */
*gen Y0_pure = 4 * treated + 0.1 * treated * (t-10) * (E_i - 9);/* 基于 E_i 的前趋势 ... */
gen eps = sqrt(0.2) * rnormal() ;
gen actual = Y0_pure + TE * treated ;
gen y = actual + eps ;/* 观察到的 Y */
end ;
cap prog drop bigone ;
prog def bigone ;
runme "10 11" 0 0 ;
forvalues i = 4/16 { ;
runme "4 16 `i' " 0 0 ;
local rest_m3_`i' = count[1,3] - 2 ;
runme "4 16 `i' 10" 0 0 ;
local rest_m4_`i' = count[1,3] - 2 ;
} ;
drop _all ;
set obs 7 ;
gen E_i = _n + 3 ;
qui gen units3 = . ;
qui gen units4 = . ;
qui forvalues i = 4/10 { ;
replace units3 = `rest_m3_`i'' if E_i == `i' ;
replace units4 = `rest_m4_`i'' if E_i == `i' ;
} ;
gen E4_i = E_i + 0.15 ;
graph twoway (scatter units3 E_i , msymbol(o) msize(medsmall))
(scatter units4 E4_i , msymbol(triangle) msize(medsmall))
,
ti("需要额外参数限制")
xtitle("E_3 的位置")
note("# DiD 限制之外需要的限制。无对照组。T=20。E_1 = 4, E_2 = 16。"
"圆圈显示 3 种单位类型，作为第三种事件日期的函数。三角形显示 4 种单位类型，其中 E_4 = 10。")
;
graph export figures/apdx_fig_A03.png , replace ;
end ;
bigone ;
|
那么，当我们需要额外约束时，可以怎么添加呢？
- 方法 1：相加为 0—— $r_1+r_2=0$
- 方法 2：等差数列—— $r_2-r_1=r_0-r_{-1}$
- 方法 3：不是论文提到的，但有确实见过这种用法：$r1=2r_2$
这种约束回归通过 cnsreg 命令实现。
附录 C：估计器的选择
目前有两种种估计器选择：
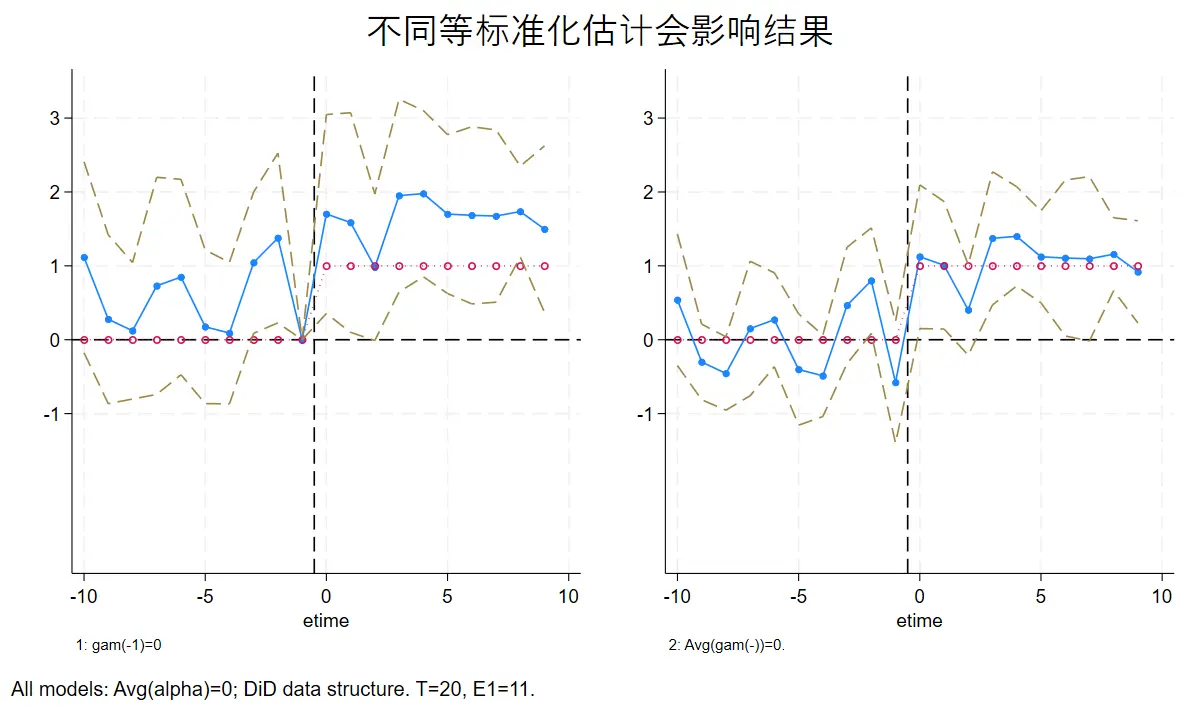
- 约束事件前一期变量的系数为 0
- 约束事前虚拟事件变量系数加总为 0
不同约束条件下的估计，两种估计都使用了个体固定效应加总为0
这部分的代码是仿真实验。
先根据条件生成处理效应，处理效应确定为 1（图中的红色线就是实际生成的处理效应）。然后加入偏差随机数，最后进行回归估计。
左侧的约束条件选择了规范化事件前一期，右侧的约束条件选择了约束事前虚拟时间变量，可以发现右侧更接近实际治疗效应（红线）。
以下代码由 GPT 进行注释，个人进行了部分修正。
代码结构：设置数据结构生成函数和约束条件选择函数，绘图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
|
#delimit ;
cap log close ;
set trace off ;
set more off ;
clear ;
set seed 2024202431 ;
cap prog drop runme ;
prog def runme ;
gendata ;
/* 创建估计变量 */
/* 事件时间虚拟变量 */
forvalues i = 0/20 { ;
gen D_p`i' = (etime == `i') ;
gen D_m`i' = (etime == -1 * `i') ;
summ D_p`i' ;
local dropme = (r(mean) == 0) ;
if `dropme' == 1 { ;
drop D_p`i' ;
} ;
summ D_m`i' ;
local dropme = (r(mean) == 0) ;
if `dropme' == 1 { ;
drop D_m`i' ;
} ;
} ;
drop D_m0 ;
gen byte group2 = E_i == 11 ;
gen trend_group2 = t * group2 ;
summ ;
/* 1 规范化事件事件-1的虚拟变量为0 */
constraint define 1 D_m1 = 0 ;
/* 2, 所有组的固定效应加总为0 */
constraint define 2 1.i + 2.i + 3.i + 4.i + 5.i +
6.i + 7.i + 8.i + 9.i + 10.i = 0 ;
/* 7 处理前的事件时间虚拟变量的平均值设为零*/
constraint define 7 D_m10 + D_m9 + D_m8 + D_m7 + D_m6 + D_m5 + D_m4 +
D_m3 + D_m2 + D_m1 = 0 ;
cnsreg y D_m* D_p*
ibn.t ibn.i , cluster(i) nocons constraints(2 1 ) collinear ;
matrix myb_ES1 = e(b) ;
matrix myV_ES1 = e(V) ;
cnsreg y D_m* D_p*
ibn.t ibn.i , cluster(i) nocons constraints(2 7 ) collinear ;
matrix myb_ES2 = e(b) ;
matrix myV_ES2 = e(V) ;
tempfile main ;
save `main' ;
/* 画图 */
*开始调试;
tempfile pooled ;
forvalues i = 0/10 { ;
drop _all ;
set obs 2 ;
gen label = "m`i'" in 1 ;
replace label = "p`i'" in 2 ;
gen etime = -1 * `i' in 1 ;
replace etime = `i' in 2 ;
foreach j in 1 2 { ;
gen cf_m`j' = . ;
/* 设置治疗效应的估计方程 */
gen truth_m`j' = (0) in 1 ;
replace truth_m`j' = (1) in 2 ;
local myb = 0 ;
cap local myb = myb_ES`j'[1,"D_m`i'"] ;
gen ES_b_m`j' = `myb' in 1 ;
local myv = . ;
cap local myv = myV_ES`j'["D_m`i'","D_m`i'"] ;
local myse = sqrt(`myv') ;
gen ES_se_m`j' = `myse' in 1 ;
local myb = 0 ;
cap local myb = myb_ES`j'[1,"D_p`i'"] ;
replace ES_b_m`j' = `myb' in 2 ;
local myv = . ;
cap local myv = myV_ES`j'["D_p`i'","D_p`i'"] ;
local myse = sqrt(`myv') ;
replace ES_se_m`j' = `myse' in 2 ;
} ;
capture append using `pooled' ;
save `pooled' , replace ;
} ;
drop if label == "m0" ;
drop if label == "p10" ;
sort etime ;
save `pooled' , replace ;
local note1 "gam(-1)=0" ;
local note2 "Avg(gam(-))=0." ;
forvalues i = 1/2 { ;
gen top_`i' = ES_b_m`i' + 1.96 * ES_se_m`i' ;
gen bot_`i' = ES_b_m`i' - 1.96 * ES_se_m`i' ;
graph twoway (connected ES_b_m`i' truth_m`i' etime , msize(medsmall medium)
msymbol(o oh) lpattern(solid dot) )
(line cf_m`i' etime , lpattern(dash) )
(line top_`i' bot_`i' etime, lpattern(dash dash) lcolor(brown brown))
, legend(off) xline(-0.5)
note("`i': `note`i''")
name(g`i' , replace) yscale(range(-3,3.5)) yline(0 , lpattern(dash) lcolor(black)) ;
} ;
graph combine g1 g2 , ti("不同等标准化估计会影响结果")
note("All models: Avg(alpha)=0; DiD data structure. T=20, E1=11.") ;
graph export figures/apdx_fig_A04.png , replace ;
end ;
cap prog drop gendata ;
program define gendata ;
/*****************
主要数据生成过程选项
/* 可能的治疗效应类型 */
1 - 零治疗效应
2 - 阶梯函数治疗效应
3 - 永久爬坡
4 - 爬坡到平台
5 - AR(1)类型
/* E_i的分布 */
T = 19; E_i ~ U(6,14)
/* 是否存在从未被处理的单位？ */
是; 否
/* Y0（潜在结果的"信号"）动态 */
1 - 基本: Y0 = 0
2 - 水平变化: Y0_i,t = E_i
3 - 趋势变化: Y0_i,t = t * E_i
主要选项结束
******************/
drop _all ;
/*
/* 经典 ES 数据结构 */
set obs 9 ;/* 组数 */
gen i = _n ;
gen E_i = 5 + i ;
gen treated = 1 ;/* 全部实验组 */
expand 20 ;/* 时间段数 */
*/
set obs 10 ;/* 组数 */
gen i = _n ;
/* NxT DiD 数据结构*/
gen treated = i > 5 ;/* 一半实验组 */
gen E_i = 11 if treated == 1 ;
expand 20 ;/* 时间段数 */
sort i ;
qui by i: gen t = _n ;
xtset i t ;
/* 创建决定 DGP 的变量 */
gen D = (t == E_i) ; /* 事件"脉冲" */
gen etime = (t - E_i) ;/* 事件虚拟时间 */
gen TE = 1 * (etime >= 0) ;/* 实验组判断 */
*gen TE = (etime >= 0) * (etime+1) ;/* endless ramp function for treatment effect */
replace TE = 0 if E_i == . ;
gen treated_post = etime >= 0 ;
gen Y0_pure = 0 + 1 * treated ;/* 偏移量 counterfactual */
*gen Y0_pure = 4 * treated + 0.3 * treated * t ;/* treated have a pre-trend ... */
*gen Y0_pure = 4 * treated + 0.01 * treated * (t-10) * (E_i - 9);/* pre-trend based on E_i ... */
gen eps = sqrt(0.3) * rnormal() ;
gen actual = Y0_pure + TE * treated ;
gen y = actual + eps ;/* observed Y */
end ;
runme ;
|
C 部分剩余部分是 Timing-based 的数据仿真实验，代码结结构式一样的，只是数据结构和约束方式不一样，这里不再重复，只放出效果图。
Timing-based结构数据
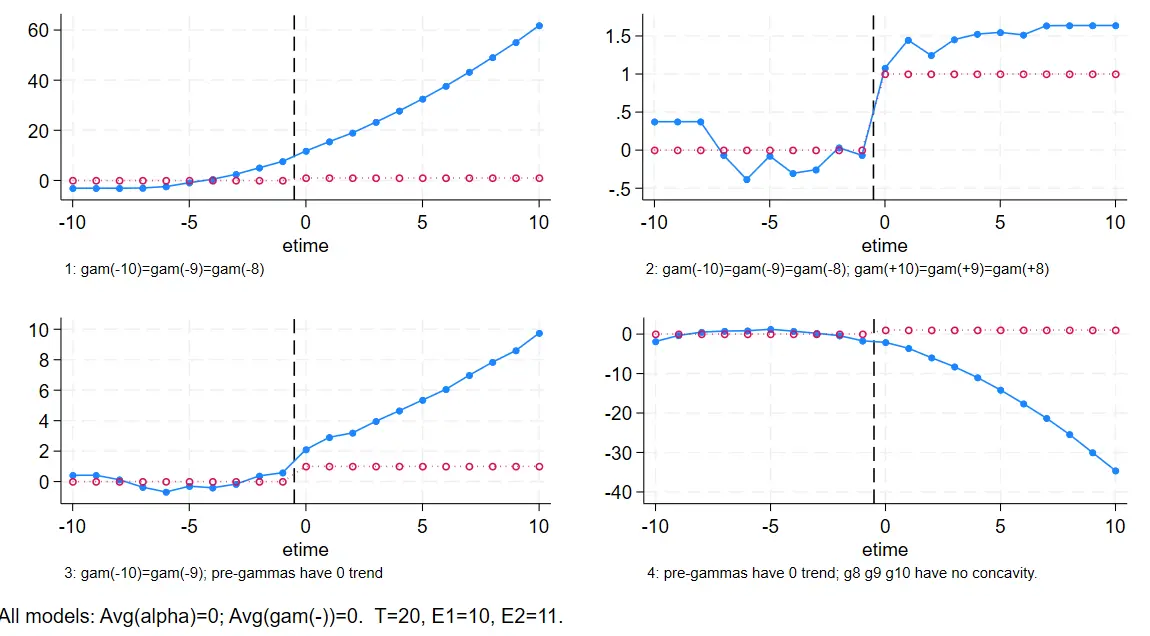
- 左上角是只约束最前期两个时间虚拟变量系数相同。
- 右上角是约束最前期三个时间虚拟变量系数相同。
- 左下角是约束事前事后最两侧三期虚拟变量系数相同。
- 右下角是约束事前预期效应虚拟变量系数加总为 0。
1
2
3
4
|
constraint define 4 D_m11 = D_m10 ;
constraint define 5 D_m10 = D_m9 ;
constraint define 6 D_m9 = D_m8 ;
constraint define 7 D_m8 = D_m7 ;
|
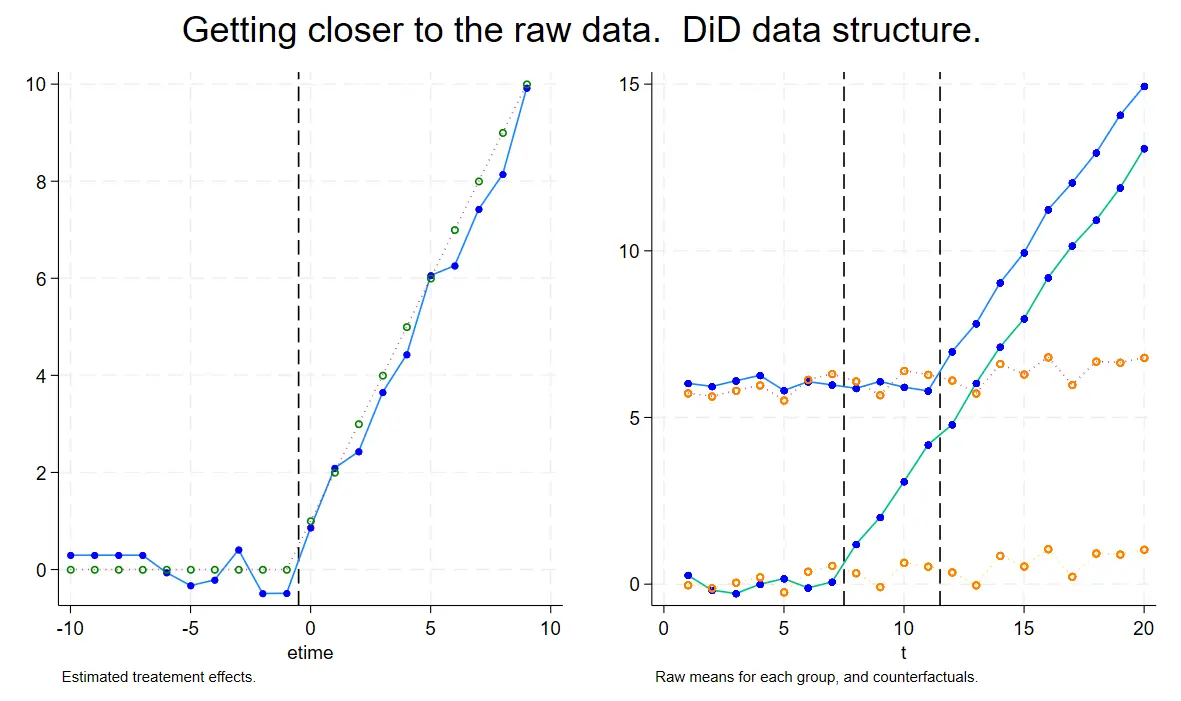
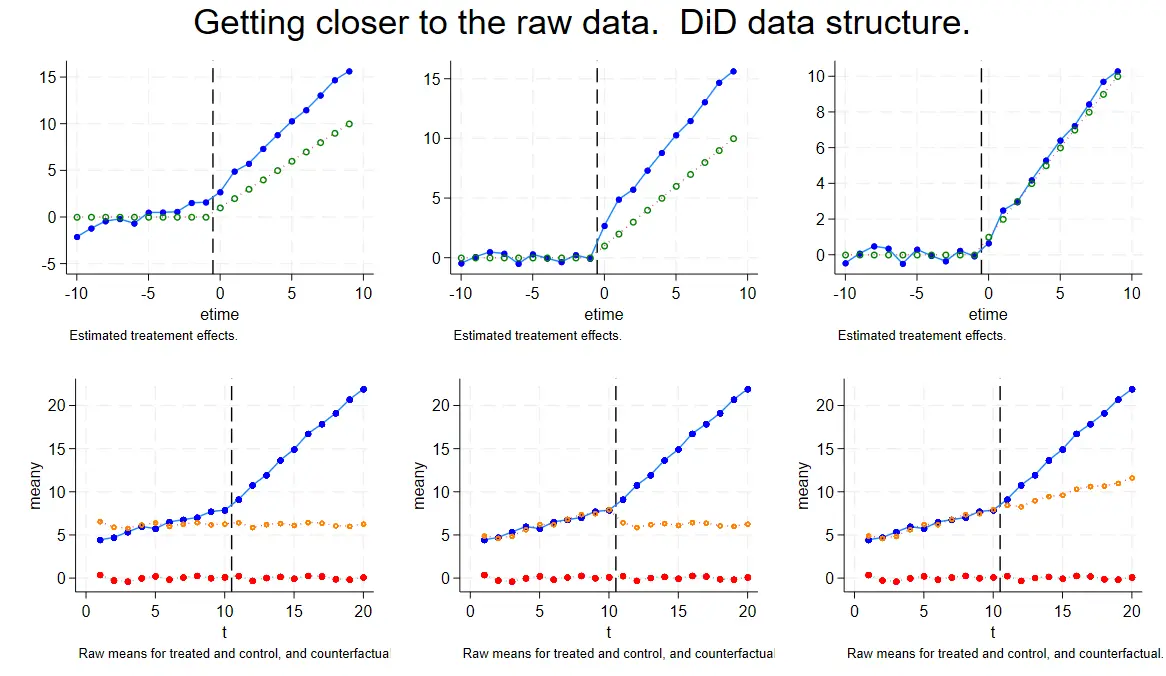
附录 D: 接近原始数据
DID 又又又封神啦🤣（
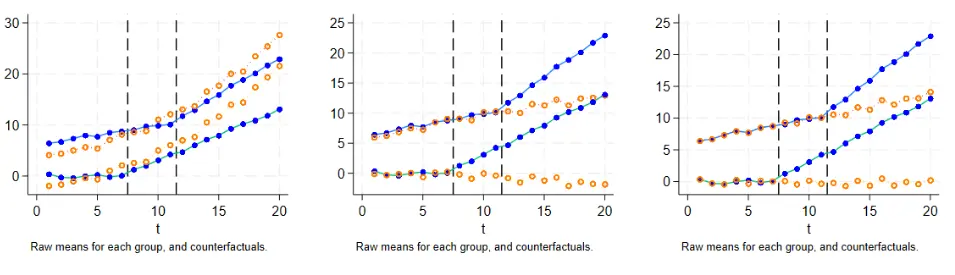
附录 D 本质可以理解为加入了时间趋势（斜率对比）的分解。和前文代码结构依旧相同，这次增加点的是反事实组的预测，通过反事实组再次对比强化因果论证。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
/* 创建反事实预测值 cf_ES2 */
gen cf_ES2 = y ; // 将 cf_ES2 初始化为观测变量 y
/* 按时间范围循环处理 */
qui summ etime ; // 求 etime 的汇总统计
local mymin = r(min) ; // 获取最小值
local mymax = r(max) ; // 获取最大值
forvalues i = `mymin'/`mymax' { // 循环遍历时间范围
if `i' < 0 { // 如果时间小于0
local j = abs(`i') ; // 取绝对值
replace cf_ES2 = cf_ES2 - _b[D_m`j'] * D_m`j' ; // 减去处理效应系数乘以对应的 dummy 变量
}
else { // 如果时间大于等于0
replace cf_ES2 = cf_ES2 - _b[D_p`i'] * D_p`i' ; // 减去处理效应系数乘以对应的 dummy 变量
}
}
/* 按单元类型和时间求反事实预测均值 */
egen meancf_ES2 = mean(cf_ES2), by(t unittype) ; // 按 t 和 unittype 求 cf_ES2 的均值
|
使用前后的系数差异再次相减得到结果
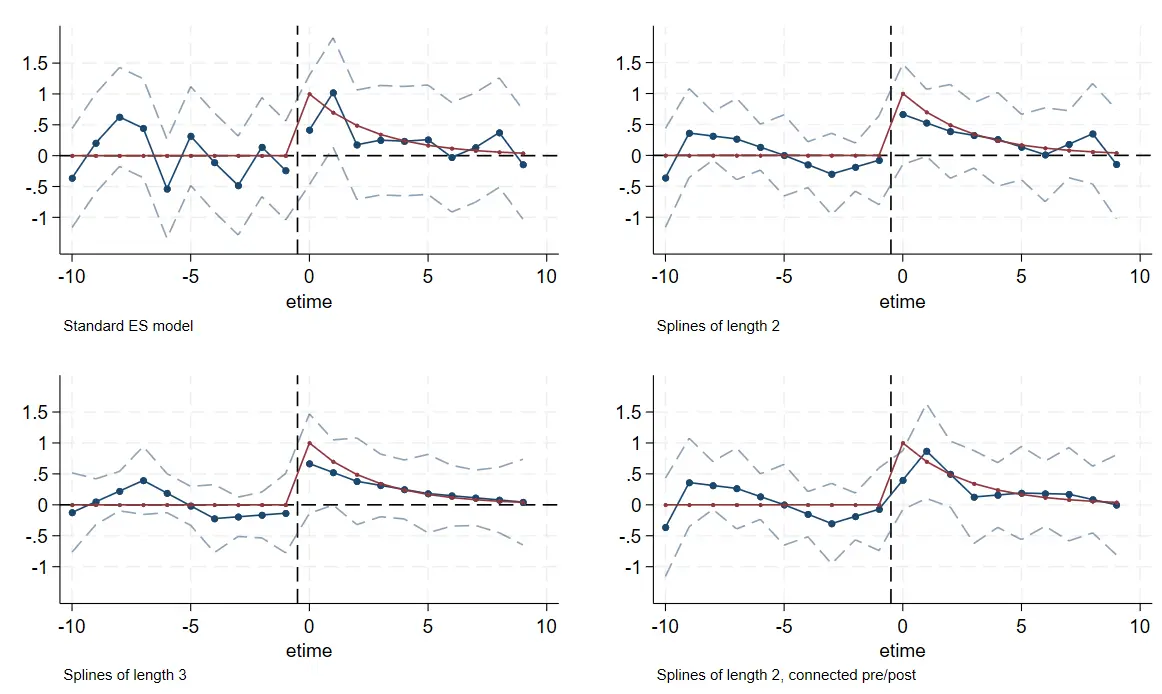
附录 E：重复的事件冲击
这部分要解决的问题是。如果一个事件在不同时间重复发生，应该如何选择。此时生成的真实处理效应是不断衰减的曲线。
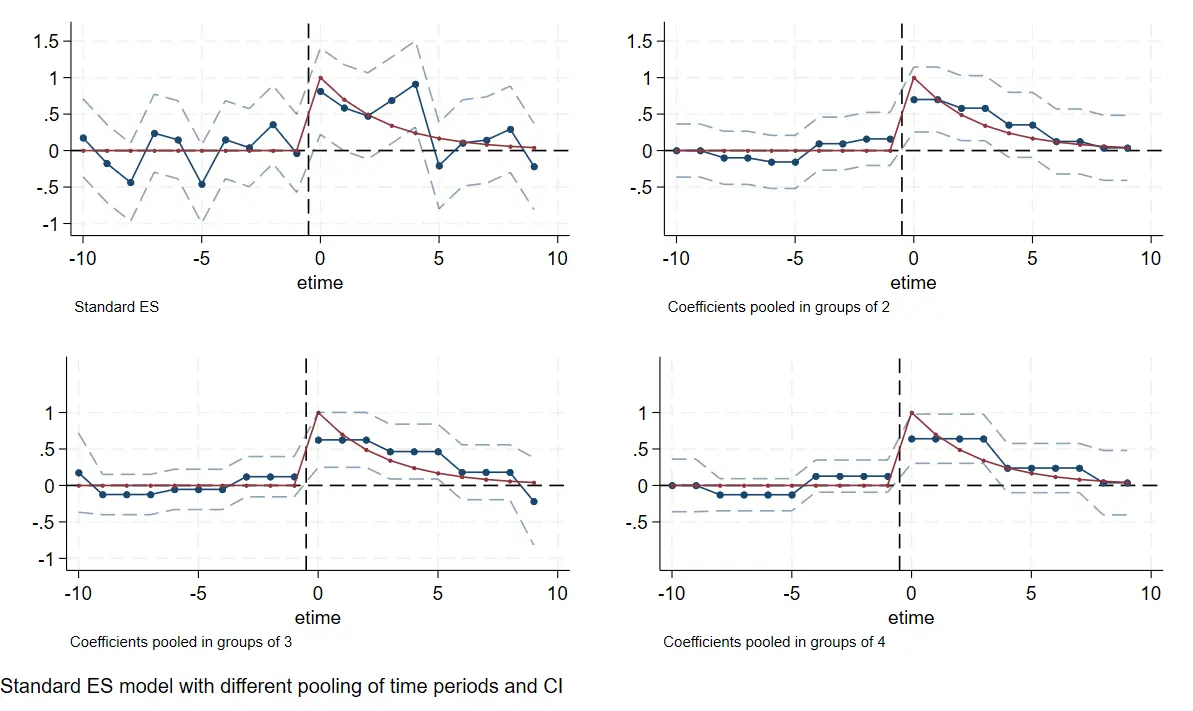
做法 1是约束事件虚拟变量的系数（$\gamma_1=\gamma_2$）相同：
如下约束就是分别为两期一组、三期一组、四期一组的分段。
以下是约束代码的例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
#delimit;
/*两期一组*/
constraint define 9 D_m10=D_m9;
constraint define 10 D_m8=D_m7;
constraint define 11 D_m6=D_m5;
constraint define 12 D_m4=D_m3;
constraint define 13 D_m2=D_m1;
constraint define 14 D_p0=D_p1;
constraint define 15 D_p2=D_p3;
constraint define 16 D_p4=D_p5;
constraint define 17 D_p6=D_p7;
constraint define 18 D_p8=D_p9;
/*三期一组 */
#delimit;
constraint define 21 D_m1=D_m2;
constraint define 22 D_m1=D_m3;
constraint define 23 D_m4=D_m5;
constraint define 24 D_m4=D_m6;
constraint define 25 D_m7=D_m8;
constraint define 26 D_m7=D_m9;
constraint define 27 D_p0=D_p1;
constraint define 28 D_p2=D_p1;
constraint define 29 D_p3=D_p4;
constraint define 30 D_p3=D_p5;
constraint define 31 D_p6=D_p7;
constraint define 32 D_p6=D_p8;
|
做法一：约束事件时间虚拟变量间的值相等
做法 2 是约束系数与系数间的斜率（$\gamma_1-\gamma_0=\gamma_2-\gamma_1$）相等
以下是约束代码的例子:
1
2
3
4
|
constraint define 9 D_m10=D_m9;
constraint define 10 D_m8=D_m7;
constraint define 11 D_m6=D_m5;
constraint define 12 D_m4=D_m3;
|
系数间都斜率相等的约束
- 左上角是普通情况。
- 右上角是两期斜率相等的分组。
- 左下角是三期斜率相等的分组。
- 右下角是事前事后两期各自相等的分组。
附录 F：时间趋势的控制
本文研究的是——是否加入时间趋势的控制和其他约束。
DID：一个个体，两个时间
两种约束，一种是加入趋势控制——控制变量加入 trend_group2
1
2
3
4
|
//趋势控制变量
gen byte group2 = E_i == 11
gen trend_group2 = t * group2 相同的约束
//其他约束类型和前文相同，保证事件虚拟时间系数相等或者斜率相等
|
施加的约束包含加入趋势控制和事件时间虚拟变量的约束
Time-based ：一个个体，两个时间
接下来验证 Time-based 数据形式
DID 形式有对照组辅助生成反事实预测，但是 time-based 缺少对照组。一般有如下几种选择：
- 事前、事末的几期事件虚拟时间系数相同，使图像更加平滑
- 事前、事末地几期事件虚拟时间系数间的斜率相同，更体现趋势
- 事前趋势系数加总约束为 0
- 多个事件时间的趋势加权约束加总为 0
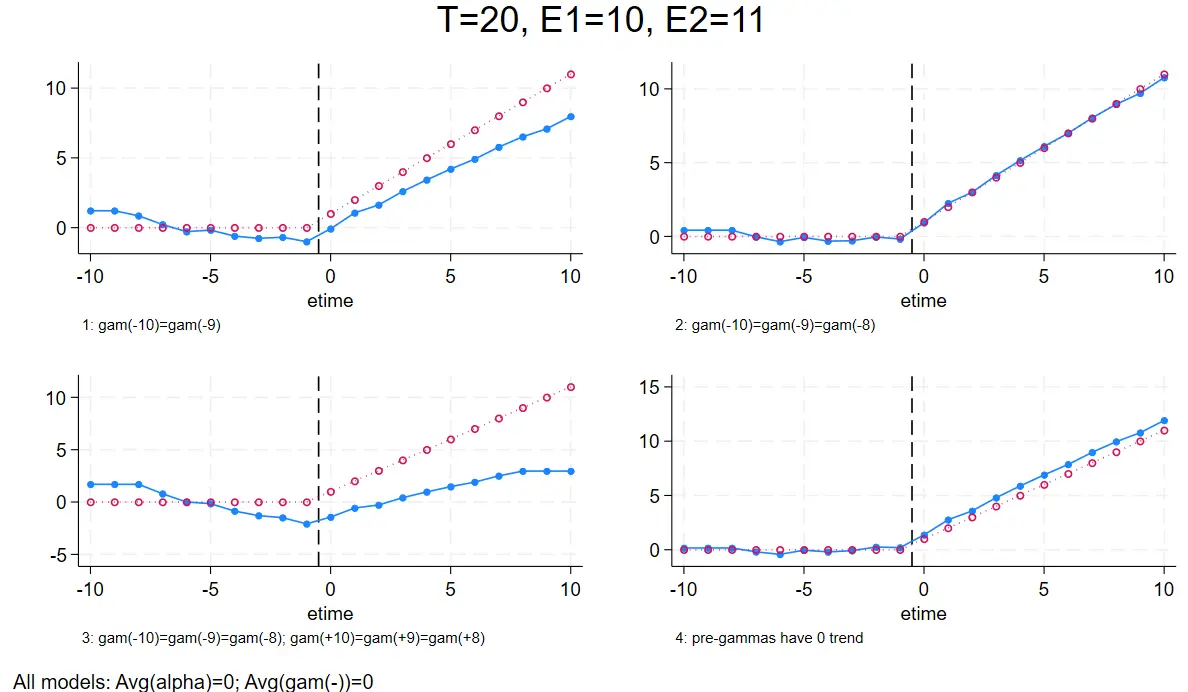
可以发现，在下图实验约束条件时，第四个图居然得出来奇怪的结果。
其施加的约束有：
- 个体固定效应加总为 0
- 事前效应加总为 0
- 事后末期斜率相同
- 加权事前趋势为 0
1
2
3
4
|
\\我没看明白这里约束5.5的基期怎么来的？
constraint define 8 (10-5.5)*D_m10 + (9-5.5)*D_m9 + (8-5.5)*D_m8 + (7-5.5)*D_m7
+ (6-5.5)*D_m6 + (5-5.5)*D_m5 + (4-5.5)*D_m4 +
(3-5.5)*D_m3 + (2-5.5)*D_m2 + (1-5.5)*D_m1 = 0 ;
|
time-based的仿真实验
那我们是选择约束系数斜率相同还是系数值相同呢？
答案是根据情况来。如果一个政策的真实效果不会随时间变动，就选择系数值相同的约束，如果政策效果随时间变动就选择系数斜率相同。
事件效果不随时间改变的跳跃冲击仿真，此时系数值相同估计更有效
个人觉得这个结论变成循环论证了。本来就是通过事件研究法估计处理效应（动态还是静态是需要我们研究的结果），现在倒变成根据结果来选择方法来。
当然，启发无非就是分析政策背景做出假设，进而选择约束方式。
DID：多个体，多时间
对于多期 DID 来说，加入多个事件时间的趋势加权约束为 0则会使得估计更加有效。如图：
第一列是普通估计，没有施加个体时间双向固定以外的限制
第二列是在第一列基础上加入了事件事前趋势加总为 0 的约束：
1
2
3
4
|
//事件日期依旧是10和5两期，个人没有看懂5.5的基期设置怎么来的
constraint define 3 -4.5*D_m10 - 3.5*D_m9 - 2.5* D_m8 - 1.5* D_m7
- 0.5*D_m6 + 0.5 * D_m5 + 1.5 * D_m4 +
2.5 *D_m3 + 3.5 *D_m2 + 4.5 *D_m1 = 0 ;
|
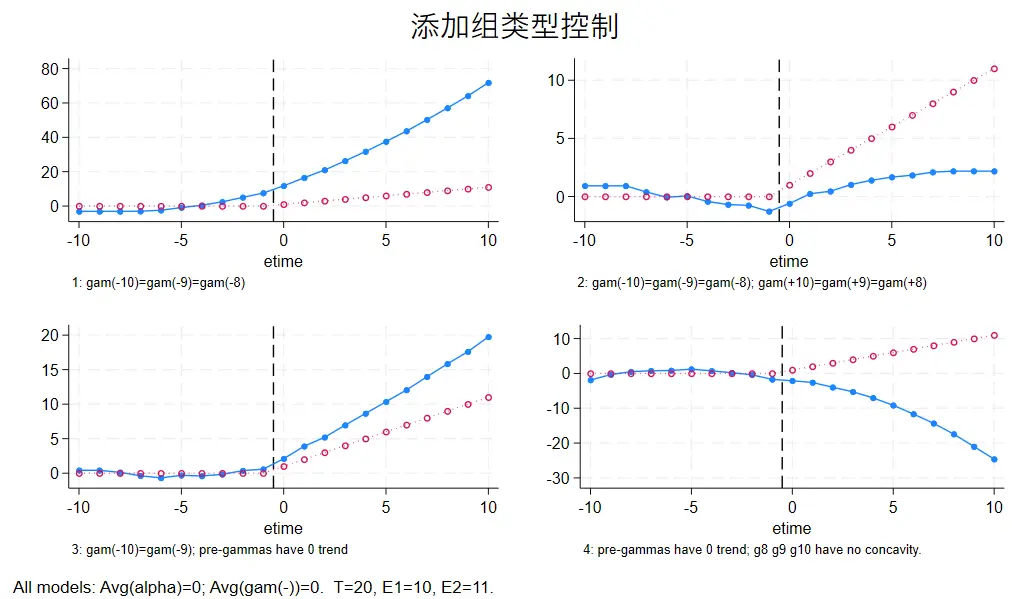
第三列是加入了类型控制
1
|
gen treated_time = treated * t
|
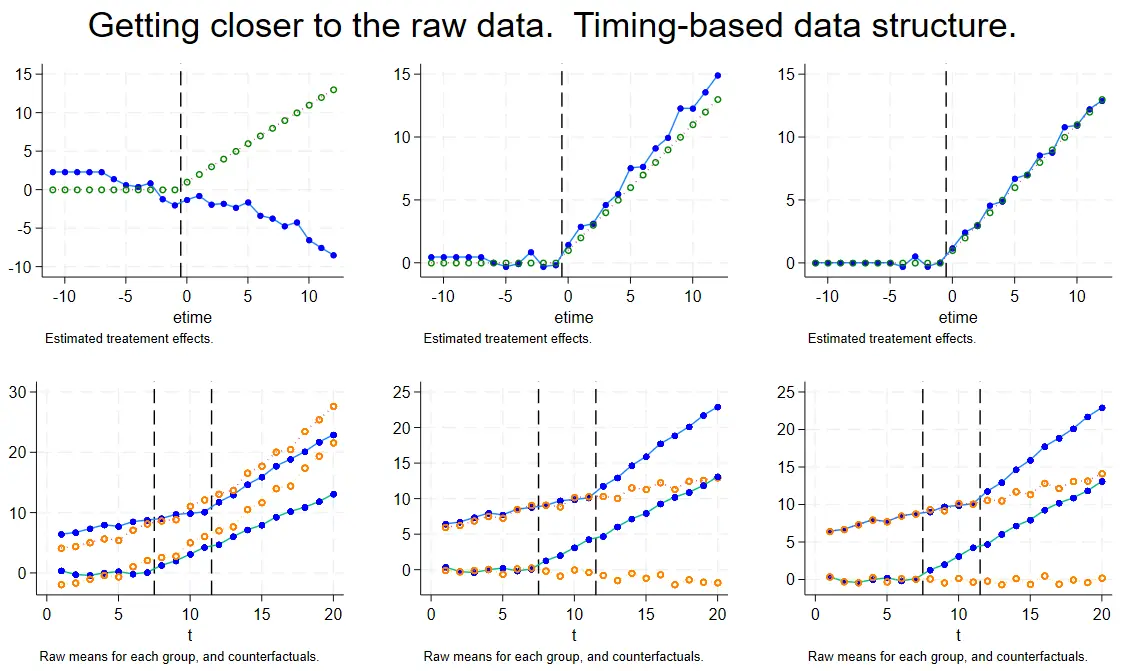
DID估计：橙色部分是基于残差预测的反事实组
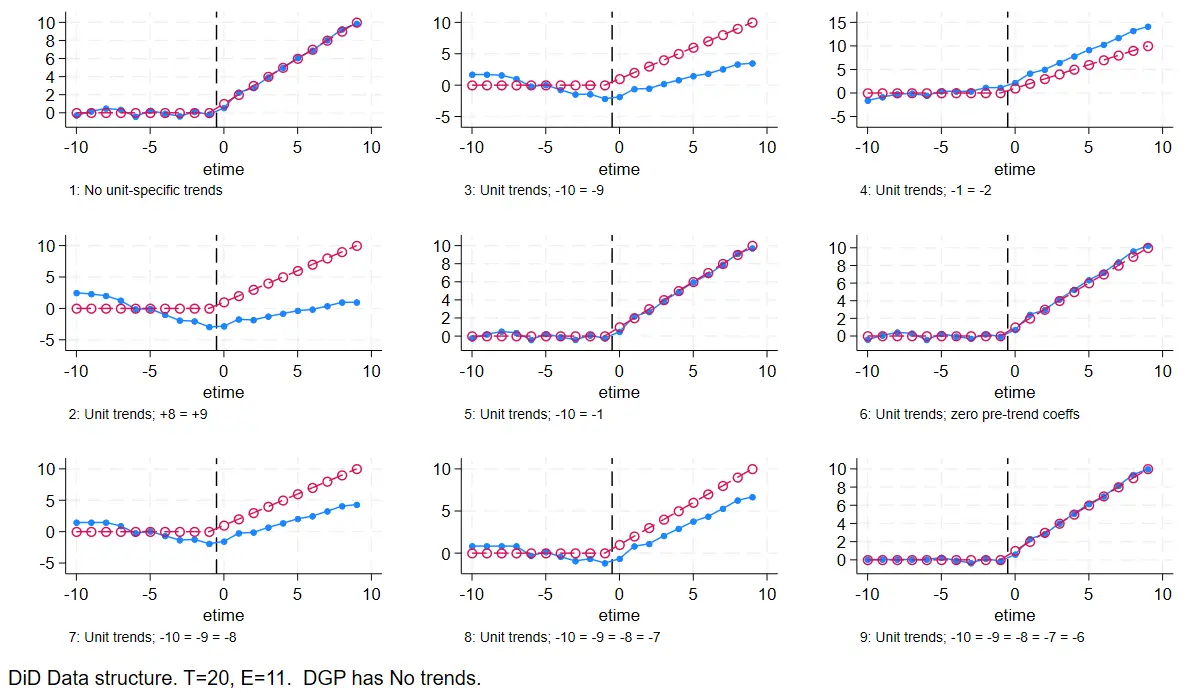
Time -based：多个体，多时间
time-based，橙色也是反事实组
上面全是实验组的 Time -based 结构中，但是这次多了个体差异。
第二列比第一列多了个体分组和时间加权趋势为 0
1
2
3
4
5
6
|
//个体分组
Egen unittype = group (E_i) ;
Egen meany = mean (y) , by (t unittype)
//时间趋势加权，我还是没看懂3.5的基期是怎么出来的
constraint define 103 (6-3.5) * D_m6 + (5-3.5) * D_m5 +
(4-3.5) * D_m4 + (3-3.5) * D_m3 + (2-3.5) * D_m2 + (1-3.5) * D_m1 = 0 ;
|
第三列比第二列多了系数约束
1
2
|
constraint define 8 D_m7 = D_m6 ;
constraint define 9 D_m6 = D_m5 ;
|
总结
事件分析法是 DID 的一种推广。
个人理解是，事件分析法会基于 DID 进一步进行时间切片。由于时间虚拟变量增多，求解也需要更多的约束，因此我们得根据研究背景添加时间趋势的控制。
- DID 和事件研究法互为补充，事件研究法能进一步展现 DID 估计的动态效应（随时间增加，减少，变异后回归正常值）。如果两种估计都方向相反，可能是由于选择了错误的约束条件，或者存在共线性的相关问题。
- 不同的数据结构，事件分析法应选择不同的额外约束数量和方式。
- 从附件代码实验来说——
- Time-based 数据集求解需要添加约束，约束的添加根据事件时间数和个体数判断。
- 事件研究法中，事前趋势标准化一般会比较准确。
- 只有一个个体、不同时间冲击的数据集，得谨慎添加约束，可能得出相反的结果。
- 多个个体的数据，无论是 time-based 还是 did，都应该加上组类别控制。
