微观经济:罗伊、霍太林、谢泼德

罗伊、霍太林、谢泼德经济计算式
《平新乔微观经济学十八讲》直接使用了上面三者作为课后试题的计算方法,但是《微观经济学:现代观点》(范里安1)中并未提到这部分知识点(数学上感觉平新乔门槛挺高的),因此在此补充记录。
《平新乔微观经济学十八讲》2在以下附件中(来自 z-library)
微观经济学十八讲 (平新乔) (Z-Library) .pdf
总体理解框架
- 谢泼德引理(Shephard’s lemma)给定生产函数数量,成本最小化;
- 罗伊恒等式(Roy’s identity)给定预算, 效用最大化;
- 霍特林引理(Hotelling’s lemma)是无约束利润函数。
他们都是包络问题的分析
一、谢泼德引理(Shephard’s lemma)
生产理论,成本最小化
给定生产函数数量,求成本最小
$$
min \sum_{i}^{n}{w_i x_i}\newline
st.\bar{y}=f(x_1,x_2 \cdots x_n)
$$
我们往往构造拉格朗日方程求解:$\mathcal{L}= \sum_{i}^{n}{w_i x_i}-\lambda[\bar{y}-f(x_1,x_2 \cdots x_n)]$
对 $x_i$ 和 $\lambda$ 求偏导等于 0,最后解出最优产量投入 $x_i$, 带入成本函数,我们就得到了最小成本3$\sum_{i}^{n}{w_i x_i^*}$。
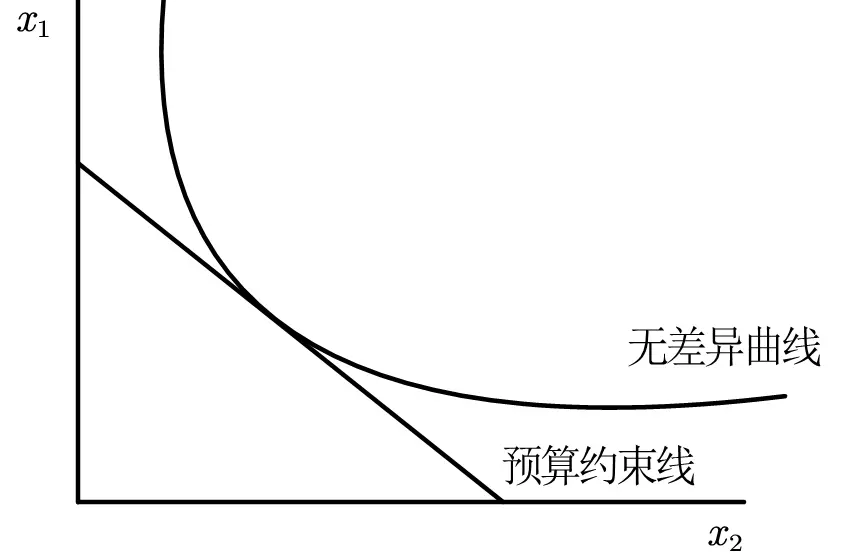
范里安教材中常用的几何求解方法为:
$$ \large \bbox[#def,10px,border: 5px solid]{\frac{\Delta x_2}{\Delta x_1}=-\frac{MP_1(x_1^{*},x_2^{*})}{MP_2(x_1^{*},x_2^{*})}=-\frac{w_1}{w_2}} $$
谢泼德引理就是拉格朗日法过程的简化。对于成本函数 $c(\mathbf{w},y)=\sum_{i}^{n}{w_i x_i^*}$ 对要素价格 $w_i$ 求偏导,方程解被称 $x_2$ 为希克斯需求函数函数(最小支出下的最优商品束)。 $$ \large \bbox[#def,10px,border: 5px solid] { x_{i}(\mathbf{w},y)=\frac{\partial c(\mathbf{w},y)}{\partial w_{i}}} $$
证明过程:
$$ \begin{align} & x_{j}(\mathbf{w},y)=\frac{\partial c(\mathbf{w},y)}{\partial w_{j}}\newline &=\frac{\partial\sum_{i=1}^{n}{w_i x_i}}{\partial w_{j}}\newline &=x_j+\color{red}{\sum_{i=1}^{n}w_i\frac{\partial x_i}{\partial w_j}} \end{align} $$
对于红色部分 $\color{red}{\sum_{i=1}^{n}w_i\frac{\partial x_i}{\partial w_j}}$,我们之前的拉格朗日方程有
$$ \frac{\partial \mathcal{L}}{\partial x_i}=w_i-\lambda f(x_1,\cdots ,x_n)=0\newline \Rightarrow w_i=\lambda f(x_1,\cdots ,x_n) $$ 把 $w_i$ 代入替换,原式变为 $$ \begin{align} &x_j+\color{red}{\sum_{i=1}^{n}w_i\frac{\partial x_i}{\partial w_j}}\newline &=x_j+\sum_{i=1}^{n}\lambda f (x…)\frac{\partial x_i}{\partial w_j}\newline &=x_j+\lambda \sum_{i=1}^{n}f (x…)\frac{\partial x_i}{\partial w_j}\newline \end{align} $$ 同时,条件有给定产量函数数值 $\bar{y}$ $$ \bar{y}=f(x_1,x_2 \cdots x_n) $$ 因此实际上,对式子 $w_j$ 导为 0。 $$ \frac{\partial\bar{y}}{\partial w_j}=\frac{\partial f(x_1,x_2 \cdots x_n)}{\partial w_j}=0 $$ 等式成立。
消费理论,同理,
要素价格变为商品价格,成本函数变成支出函数。
给定价格效用,最小成本问题的需求 $x_i^*$ 的解 ,我们把其叫做希克斯需求函数。
$e(p,u)$: 给定的支出函数。 $$ \large \bbox[#def,10px,border: 5px solid]{x_i^h=h_i(p,u)=\frac{\partial e(p,u)}{\partial p_i}} $$ 使用条件:$e(p,u)$ 可微,$w_i>0$。
应用举例
总成本函数为:$C=qv^{2/3}v^{1/3}$
(1)利用谢泼德引理计算 kk 和 ll 的要素需求函数
(2)根据(1)的结论计算潜在生产函数
(1)
$$ \begin{aligned} l&=\frac{\partial C}{\partial w}=\frac{2}{3}q\bigg(\frac{v}{w}\bigg)^{1/3} \newline k&=\frac{\partial C}{\partial\nu}=\frac{1}{3}q\bigg(\frac{w}{\nu}\bigg)^{2/3} \end{aligned} $$ (2)根据(1)的结果消除 $\frac{v}{w}$, $q=\left(\frac{3}{2}\right)^{2/3}(3)^{1/3}l^{2/3}k^{1/3}=Bl^{2/3}k^{1/3}$。
$B=\left(\frac{3}{2}\right)^{2/3}\left(3\right)^{1/3}$。
二、罗伊恒等式(Roy’s identity)
消费理论, 效用最大化
给定预算约束线,求效用最大化
$$ \max u=f(x_1,x_2 \cdots x_n) \newline st.\sum_{i=1}^{n}{x_ip_i}=m $$
范里安中常用的几何求解方法为:
$$ \large \bbox[#def,10px,border: 5px solid]{\frac{\Delta x_2}{\Delta x_1}=-\frac{MU_1(x_1^{*},x_2^{*})}{MU_2(x_1^{*},x_2^{*})}=-\frac{p_1}{p_2}} $$
间接效用函数 ${\displaystyle v(\mathbf {p} ,w)}$:满足预算约束时的最大效用
$\mathbf {p}$ : 商品价格, $w$ :工资
则商品需求数量的解 $x_i$ 也就是马歇尔需求函数(商品价格与需求的函数)。 $$ \large \bbox[#def,10px,border: 5px solid] {x_i^m=-\frac{\partial v/\partial p_i}{\partial v/\partial m} } $$ ($x_i^m$ 中的 m 表示的是马歇尔需求函数的意思,同理, $x_i^h$ 中的 h 是希克斯需求函数。)
证明过程:
拉格朗日函数为 $\mathcal{L}=u(\mathbf{x})-\lambda(\mathbf{p}\cdot\mathbf{x}-m)$,对 $\mathcal{L}$ 求 $x_i$ 偏导。 $$ \frac{\partial\mathcal{L}(\mathbf{x}^{f},\lambda^{f})}{\partial x_i}=\frac{\partial u(\mathbf{x}^{f})}{\partial x_i}-\lambda^{f}p_i=0 $$ 对于拉格朗日函数,我们对预算上限 $m$(这里指收入)求导
$$ \frac{\partial\mathcal{L}(\mathbf{x}^{f},\lambda^{f})}{\partial m}=\lambda^{f} $$ 如何理解 $\lambda$ ——它是影子价格。
$$ \boxed{\max u=f(x_1,x_2 \cdots x_n)\newline st.\sum_{i=1}^{n}{x_ip_i}=m\newline } $$ $$ \mathcal{L}=u(\mathbf{x})-\lambda(\mathbf{p}\cdot\mathbf{x}-m) $$ 当我们改变约束条件$.st$ 里的 $m$ 的值时,也就是产生 $\Delta m$ 的变化,目标函数 $\max u$真正被改变的值是。$\lambda^f\Delta m$ 因此我们说 $\lambda$ 衡量了对应要素的改变对于真正目标函数的变化,被叫做“影子价格(真实价格)”。
由此我们得到:
$$ \lambda={\frac{\partial{\mathcal{L}}}{\partial m}}={\frac{\partial v (\mathbf{p},m)}{\partial m}} $$ 同理,如果我们研究 p 的变化,可以得到
$$ \frac{\partial\nu(\mathbf{p},m)}{\partial p_{i}}=\frac{\partial\mathcal{L}(\mathbf{x}^{f},\lambda^{f})}{\partial p_{i}}=-\lambda^{f}x_{i}^{f} $$ 联立, $$ \begin{cases} \lambda={\frac{\partial v (\mathbf{p},m)}{\partial m}}\newline \frac{\partial v(\mathbf{p},m)}{\partial p_{i}}=-\lambda^{f}x_{i}^{f} \end{cases} $$ 得到罗伊恒等式。
应用举例
平新乔《微观经济学十八讲》第 16 讲“一般均衡与福利经济学的两个基本原理”
第 3 题
考虑两个消费者,两种商品的经济,消费者效用禀赋如下。
$$ \begin{aligned} u^{1}(x_{1},x_{2})&=\min{x_{1},x_{2}}&e^{1}=(30,0) \newline \nu^{2}\left(p,y\right)&=\frac{y}{2\sqrt{p_{1}p_{2}}}&e^{2}=(0,20)\end{aligned} $$ 求发现瓦尔拉斯均衡
消费者 1 的马歇尔需求: $$ x_{1}^{1}=x_{2}^{1}=\frac{m}{p_{1}+p_{2}}=\frac{30p_{1}}{p_{1}+p_{2}} $$ 消费者 2,使用罗伊恒等式 $x_{i}\left(p,m\right)=-\frac{\partial\nu/\partial p_{i}}{\partial\nu/\partial m}$ 得到:
$$ x_{i}^{2}=\frac{m}{2p_{i}}=\frac{10p_{2}}{p_{i}} $$ 解得——略
三、霍特林引理(Hotelling’s lemma)
谢泼德引理和罗伊恒等式都是由约束条件下的包络问题,霍特林引理则是无约束情况下的包络问题。
生产理论,利润最大化
给定利润函数
$$ \pi(p)=\max_{x}p\cdot f\small{(x(p,w))}-w\small{x(p,w)} $$ $w$:生产要素价格,$ y (p)$ : 厂商供给函数, $y(p)\triangleq f(x(p))$ 为净供给量。
范里安里这类题先判断是完全竞争还是非完全竞争、短期、长期、要素、商品市场。
霍特林引理为: $$ \large \bbox[#def,10px,border: 5px solid] {y^{*}(p)=\frac{d\pi(p)}{dp} } $$
证明过程:
对于 $$ \pi(p)=\max_{x}p\cdot f\small{(x(p,w))}-w\small{x(p,w)} $$ 一阶最大化条件为: $$ p\frac{\mathrm{\partial}f(x(p,w))}{\mathrm{\partial}x}-w=0 $$ 利润函数 $\pi$ 对 p 求导: $$ \frac{\partial\pi(p,w)}{\partial p}=f(x(p,w))+\color{blue}{p\frac{\mathrm{d}f(x(p,w))}{\mathrm{d}x}\cdot\frac{\partial x(p,w)}{\partial p}-w\frac{\partial x(p,w)}{\partial p}} $$
$$ \color{blue}{蓝色部分=(p\frac{\mathrm{\partial}f(x(p,w))}{\mathrm{\partial}x}-w)\frac{\partial x(p,w)}{\partial p}}=0 $$
应用举例
平新乔《微观经济学十八讲》第七讲“要素需求函数、成本函数、利润函数与供给函数”
第一题
已知生产函数为 $f(x_1,2_2)=0.5lnx_1+0.5lnx_2$ 求利润函数 $\pi(w_1,w_2,p)$, 并用两种方法求供给函数。
利润函数: $\pi=\frac{p}{2}(lnp^2-ln4w_1w_2)-p$
供给函数:使用 Hotelling’s lemma $$ y=\frac{\partial\pi(w_1,w_2,p)}{\partial p}=\frac{1}{2}(lnp^2-ln4w_1w_2) $$ 普通方法,分别求偏导 $\frac{\partial \pi}{\partial x_i}=0$ 解出 $x^*$, 带入利润函数,答案相同。
四、补充
参考数理经济学的基本方法(蒋中一),这几个定理其实就是基于包络分析求出间接函数。
将间接函数代入这类问题的一阶条件消除参数 𝜆 ,就会得到范里安中常见的图形解。
给定成本,利润最大化;给定利润,成本最小化。两者互为对偶问题,函数结果相同,但包络分析下的参数 𝜆 互为倒数。