马尔萨斯两部门模型

课堂展示使用，《富种起源》部分数理推导细节。

问题的悬赏

《富种起源》作者的博士论文，希望高中生也能阅读，这里只介绍简化版的古典模型。

这本书是为了反驳主流马尔萨斯机制而写的书。宏观的经济史、经济增长的魅力在于——通过简洁的模型塑造一种 史观 。

吴乐旻的《富种起源》论证说马尔萨斯对马尔萨斯陷阱的解释是错误的，那么马尔萨斯陷阱真正的原因是什么？

反驳的悬赏如下：

马尔萨斯叙事

马尔萨斯是人资环学科的鼻祖。

一种经济增长叙事

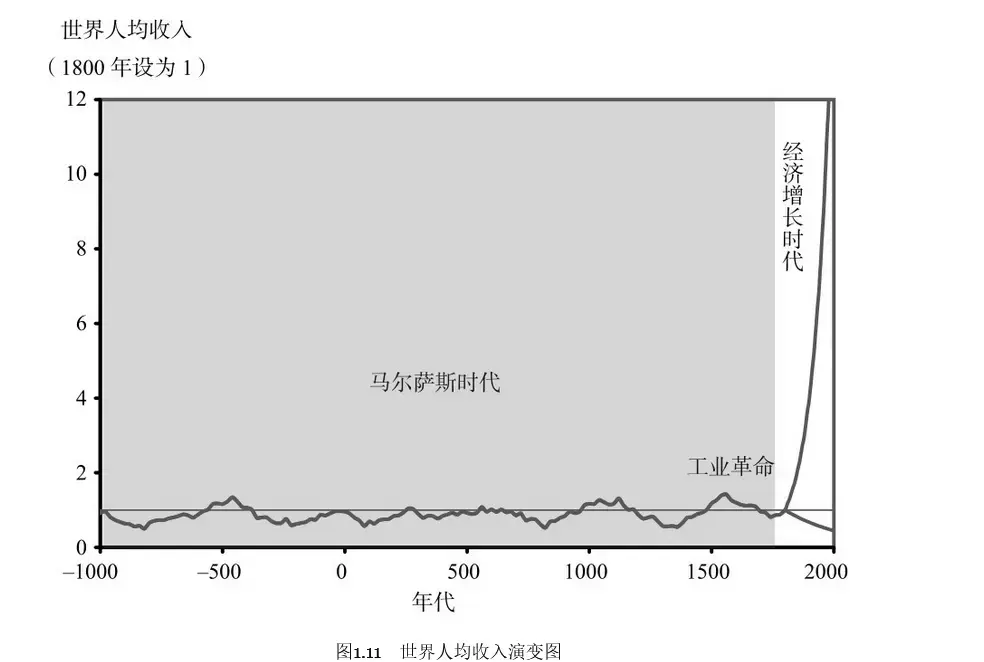
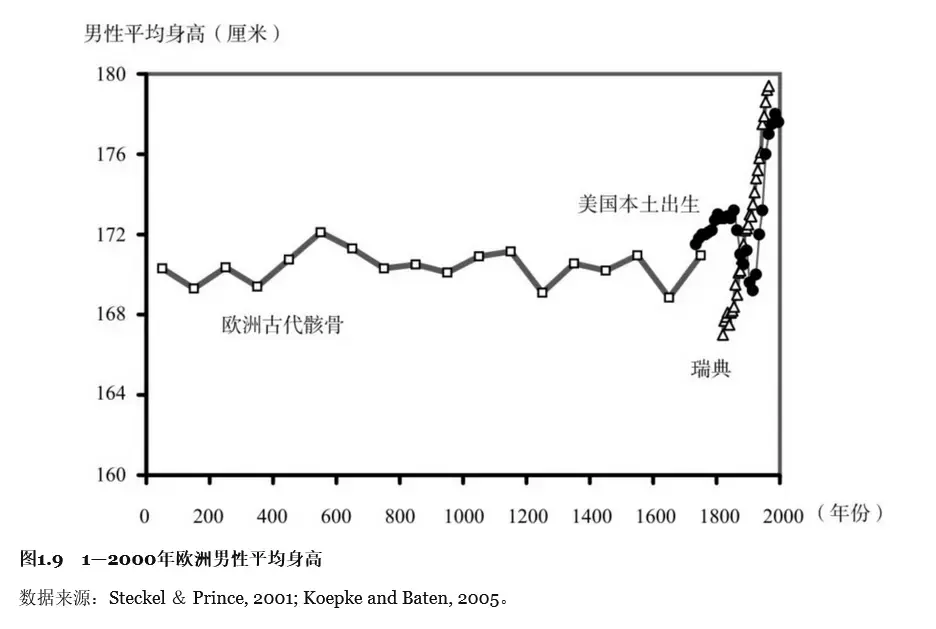
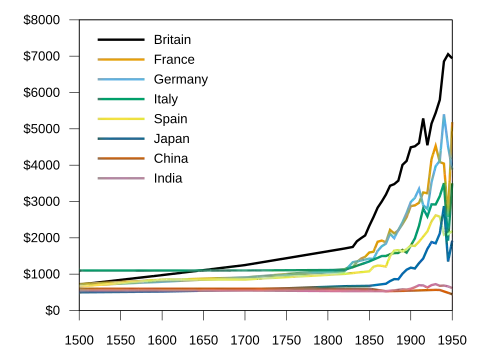
在漫长的经济增长史中，似乎只发生了一件事——工业革命。 ——格里高利·克拉格（Gregory Clark）

• 明朝的人均实际收入和宋朝的实际收入难道一样?
• 繁荣如果完美，为何不能持续？
• 为何历史总在民主和不民主间摇摆。
• 为何工业革命能破坏马尔萨斯陷阱？
• 能不能用一个大一统模型描述整个经济增长史？

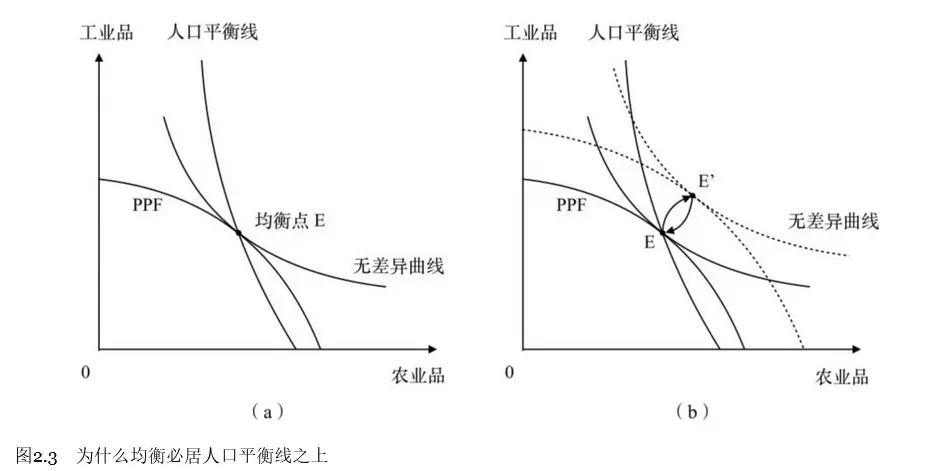
两部门模型

先分析部门进步和社会福利。

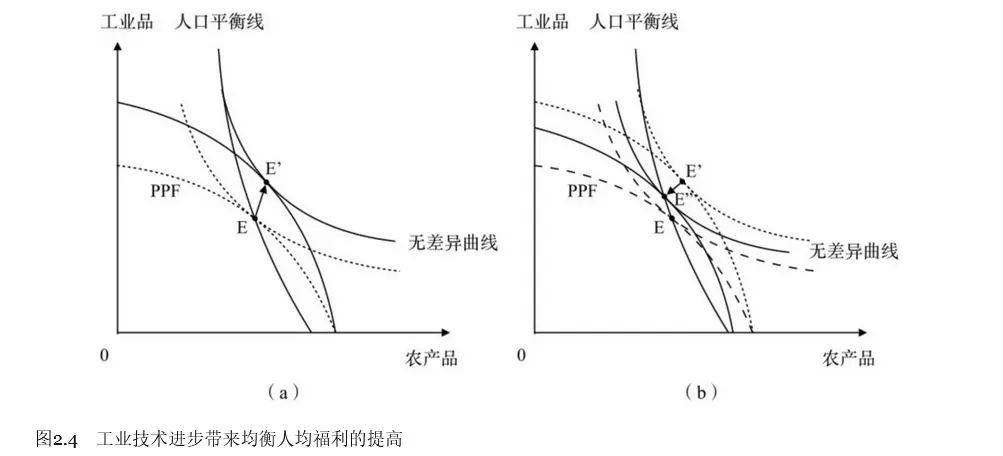
两个部门同时进步的情况：

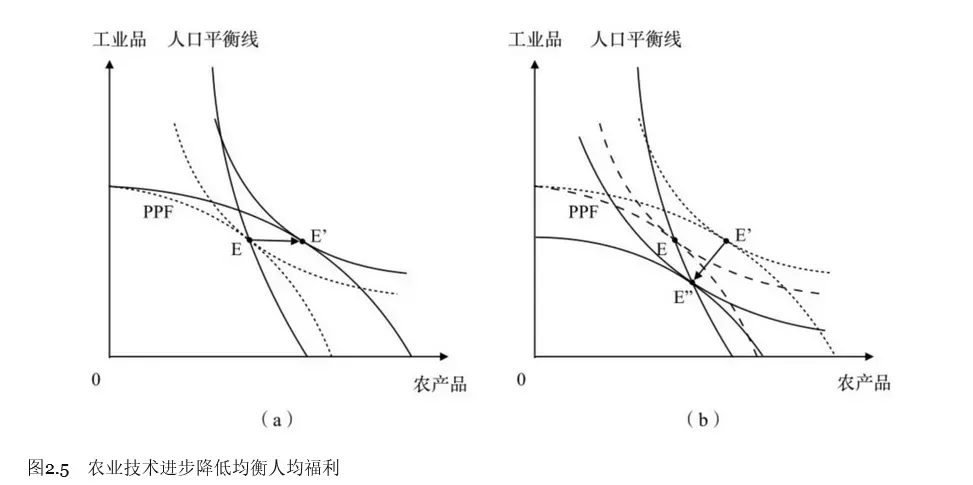
只有工业部门进步的情况：

只扩张工业部门，等比例萎缩。

只扩张工业部门，等比例萎缩。

改变偏好

类比月亮和六便士，接下来把工业、农业转化成效用、生存两个部门。

• 效用部门：艺术、文学、玫瑰……
• 生存部门：国防、工科、大米……

人们更偏好效用品，生育率暂时偏离（减少侧），提升社会福利。

社会福利增加影响因素；

• 效用品和生存品部门进步率。
• 偏好结构。
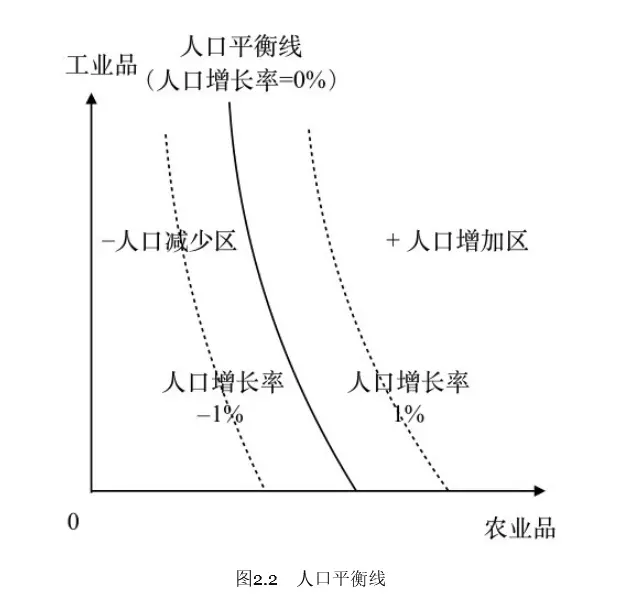
• 人均消费（人口平衡线）

模型代数证明（简单情况）

$$ \max U(x,y)=x^{1-\beta}y^\beta $$

$$ \begin{cases} \text{生存部门:}X=AL_A^{1-\gamma_A}H_A^{\gamma_A} \\ \text{效用部门:}Y=BL_B^{1-\gamma_B}H_B^{\gamma_B} \end{cases} $$

假设 1：$\gamma_A=\gamma_B\equiv\gamma<1$（如果放松）

$$ \max U(x,y)=x^{1-\beta}y^\beta $$

$$ \begin{cases} \text{生存部门:}&X=AL_1^{1-\gamma}H_1^\gamma\\ \text{效用部门:}&Y=BL_2^{1-\gamma}H_2^\gamma\\ \text{土地:}&L_1+L_2=L\\ \text{劳动:}&H_1+H_2=H& \end{cases} $$

接下来求解：逆向归纳——社会决策—— 效用 —— 产品 —— 要素。

需要决定的要素是为每个产品消耗多少要素。

$$L_2=L-L_1,\quad H_2=H-H_1$$

$$ U=(AL_1^{1-\gamma}H_1^{\gamma})^{1-\beta}[B(L-L_1)^{1-\gamma}(H-H_1)^{\gamma}]^{\beta} $$

取对数后处理更简单一些：

$$ V=(1-\beta)\left[\ln A+(1-\gamma)\ln L_1+\gamma\ln H_1\right]+\beta\left[\ln B+(1-\gamma)\ln\left(L-L_1\right)+\gamma\ln\left(H-H_1\right)\right] $$

最优化即偏导为 0。 $$ \frac{\partial V}{\partial L_1}=\frac{(1-\gamma)(1-\beta)}{L_1}-\frac{(1-\gamma)\beta}{L-L_1}=0 $$ $$ L_1^*=(1-\beta)L,\quad L_2^*=\beta L $$ 同理，

$$ \frac{\partial V}{\partial H_1}=\frac{\gamma(1-\beta)}{H_1}-\frac{\gamma\beta}{H-H_1}=0 $$ $$H_1^*=(1-\beta)H,\quad H_2^*=\beta H$$ 要素决策后，接下来代入产品决策 $X=AL_1^{1-\gamma}H_1^\gamma$。

$$ \begin{aligned}X^{*}&=A\left(L_{1}^{*}\right)^{1-\gamma}(H_{1}^{*})^{\gamma}=A[(1-\beta)L]^{1-\gamma}[(1-\beta)H]^{\gamma}\\&=A\left(1-\beta\right)L^{1-\gamma}H^{\gamma}\end{aligned} $$ 人均水平再除以 H,

$$ \begin{cases}x=A(1-\beta)\left(\frac{H}{L}\right)^{\gamma-1}\\y=B\beta\left(\frac{H}{L}\right)^{\gamma-1}&\end{cases} $$ 产品决策后，代入效用 $U=x^{1-\beta}y^{\beta}$，

$$ \begin{aligned}\mathrm{U}&=A\left(\frac{H}{L}\right)^{\gamma-1}\left(\frac{B}{A}\right)^\beta(1-\beta)^{1-\beta}\beta^\beta\\&=x\left(\frac{B}{A}\right)^\beta\left(\frac{\beta}{1-\beta}\right)^\beta\end{aligned} $$

假设 2： $g_H\equiv\frac{\dot{H}}{H}=n=\delta\left(\ln x-\ln\bar{x}\right)$

马尔萨斯陷阱的描述。

微分方程——导数与数值的关系——增量和存量的关系——动态方程。

$\bar{x}$ 是使人口保持不变的平均生存品消费水平。

结论一

均衡效用的表示：

$$ U^E=\bar{x}\left(\frac{B}{A}\right)^\beta\left(\frac{\beta}{1-\beta}\right)^\beta $$

均衡人均效用随着产出结构效用品化程度（$\frac{B}{A}$ ）、对效用品的相对偏好（ $\beta$）和维持人口平衡所需的人均生存品消费（$\bar{x}$ ）的增长而增长。

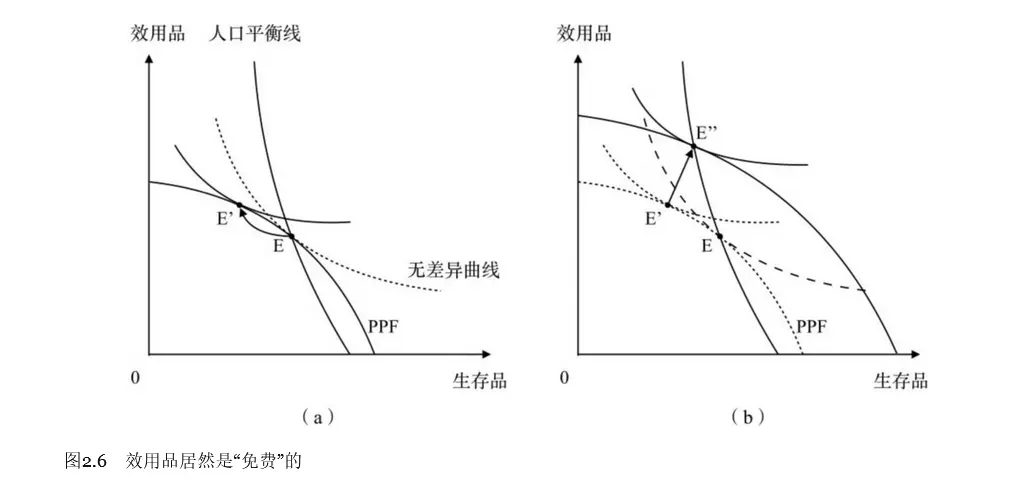
尚未证明的图示情况：

不同部门增长速度与社会福利的关系。

为保持模型简单，只考虑封闭的社会，不存在对外贸易。

生存产品的增长速度为 $g_A$ ；效用产品的增长速度为 $g_B$ 。

引理 ：$g_A-(1-\gamma)g_H\to0$

马尔萨斯人口增长的假设：$g_H\equiv\frac{\dot{H}}{H}=n=\delta\left(\ln x-\ln x\right)$

均衡人均消费的情况：$x=A(1-\beta)\left(\frac{H}{L}\right)^{\gamma-1}$

土地资源简化为 1，得到 $x=A(1-\beta)^{\gamma}H^{\gamma-1}$，代入 $g_H$:

$$ g_H=\delta\left[\ln A+\gamma\ln(1-\beta)+(\gamma-1)\ln H-\ln x\right] $$

使用 M 指代 $\ln A+\gamma\ln(1-\beta)$，简化为：

$$g_H=\delta\left[M+\gamma\ln(1-\beta)-\ln x\right]$$

对 M 进行微分，

$$ \mathrm{d}M=g_A+(\gamma-1)g_H=g_A+(\gamma-1)\delta\left[M+\gamma\ln(1-\beta)-\ln x\right] $$ 稳态时，$dM=0$, 代入求解，

$$ M^*=\frac{g_A}{(1-\gamma)\delta}-\gamma\ln(1-\beta)+\ln\bar{x} $$

而此时又有：$\mathrm{d}M=g_A+(\gamma-1)g_H=0$

$M$ 趋于均衡的 $M^*$ 的过程就是 $dM$ 靠近 0 的过程。

定理三：人均效用增长率和两个部门的增长率

研究人均效用增长率（也可以看作人均收入），和两个部门增长的关系。

宏观的平衡增长路径，相图分析就是这种。

在偏离稳态的地方（$\bar{x} \neq x$）,

效用为:

$$ U=A\left(\frac{H}{L}\right)^{\gamma-1}\left(\frac{B}{A}\right)^{\beta}(1-\beta)^{1-\beta}\beta^{\beta} $$

取对数求导线性化，即可得到：

$$g_U=\beta\left(g_B-g_A\right)+g_A-(1-\gamma)g_H$$ 后面即为引理部分，已经证明了趋于 0。

于是得到了人均福利（收入）与生存品和效用品的关系。

$$ g_U=\beta\left(g_B-g_A\right) $$ 按照这个结论，人均收入长期停滞的原因应该只有一个，

效用品的增长速度总是无法高于生存品的增长速度。

更复杂的情况会引入人口迁移与贸易（通过设定人口迁移率来满足人口平衡线）、技术竞争（需要一些随机过程的数学），直觉上通过多层次博弈(《三体：黑暗森林》)理解即可，这里不再展开具体的数理模型。

后半部分简单解读参见：

竞择理论