制度、政治、民主与阿罗不可能定理

制度是经济增长的根本原因——诺斯
我一直想找机会记录下我在财政课上第一次接触到“新政治经济学”的震撼。现在决定梳理一番是基于以下原因:
- 学了测度论后,有了一点点泛函基础(其实不需要)
- 组会上老师聊到了一点国内政策执行现状,提到政治经济学确实是一个很重要的视角。我也十分赞同。制度激励是一个相当有趣的研究领域。
- 2024 年诺奖理由是制度经济学、政治经济学的贡献
- 美国大选的精彩反转
- B 站刷到了相关视频
- 马上要忙起来了,现在不写就没时间了
从制度到政治经济学
两个问题:
- 国家的起源是什么(财政的本质是什么?)
- 什么决定了国家的发展路径?
我经常在博客里用这个问题举例1——政府起源是什么?一种流派是古典政治经济学,以社会契约论、公共物品论2、社会福利理论为代表。权力集体的设置源于集体最优化的需求。
当然,如何衡量社会福利本身也是一个哲学问题,最小值(无知之幕思想实验3)?最大值?均值?绝对值?边际值?设计加权的凸函数?
在此之上,正义的价值观也是哲学问题,例如阿马蒂亚森(Amartya Sen)的选择自由;计划经济的结果平均;初始分配的禀赋平均……
税收设置就像电车难题,一条路上是穷人,一条路上是中产阶级,一条路上是富人——甚至驾驶员得考虑一些人会在被撞前变身超级赛亚人掀桌子。
在引入另一个流派前,我们先看看下一个问题——什么决定了国家的发展。
一大流派是国际贸易视角下的资源禀赋理论。一号国家既有 4 个 a 资源,又有 2 个 b 资源,但 a 产业赚钱更多,自然就会选择 a 产业。二号国家只有 0.5 个 a 资源,又有 1 个 b 资源,因此 b 产业赚钱更多,于是发展 b 产业。
| A 资源数量 | B 资源数数量 | 更赚钱的产业选择 | |
|---|---|---|---|
| 一号国家 | 4 | 2 | A |
| 二号国家 | 0.5 | 1 | B |
因此,即便一号国家什么资源都比二号国家强,但由于它内部集中发展 A 产业最赚钱,于是他选择 A 产业;同样,二号国家选择 B 产业。这个模型(H-O 比较优势)能形象地解释为什么绝对优势更低的弱国依旧能向强国出口商品。林毅夫教授就是在这一思想上提出来“新结构经济学”。
第一阶段看法:绝对优势
第二阶段看法:比较优势
第三阶段看法:规模效应
第四阶段看法:异质性企业
也就是说,这一流派,假定国家发展是区域资源决定的。
以下关于制度经济学的区分,参考了《制度与经济增长》(姚洋),这本书是关于姚洋教授和制度经济学大师诺斯的交流对话。(尚未看完,看完再来补充)
制度经济学并不这么认为。比如诺斯认为,所谓投资、教育、资本积累等不是经济增长的原因,而是增长的表现。如果只是堆生产要素就能实现发展,理论上讲所有国家都能模仿,但现实并非如此,实际上有效率的组织才是实现发展的主要动因。
同时,禀赋资源说总考虑人们会理性地使得自己资源优势最大化,那么举一个简单的反驳例子——逆全球化趋势也在全球局部出现。
例子 1. 科斯使用交易成本解释企业的起源——从制度层面解释了企业的产生。这说明制度的产生有所共性,而不是资源禀赋产生了特别的秩序。
例子 2. 我更想用人类学的一种观点解释制度经济学——我们的文化行为可以被看作一种过度仪式4。例如腊肉,过去腊肉作为过年的食物是因为便于保存,受到资源限制而产生的行为,但如今资源丰富了,腊肉的意义成为了新年美食的化身。
例子 3. 局部逆全球化趋势。特朗普希望制造业回流,我国强调国家安全,基于极限情况考虑战略部署,希望产业链全面发展。
例子 4. 路径依赖。例如铁路的宽度、录像机的 VHS 制式都是因为当时技术局限,在当代来看都不是最优选择,但被保留了下来。这种制度惯性也就是诺斯口中的“历史是有意义的”。
例子 5. 正式会议要穿西服;结婚需要彩礼;探病最好不要空手…… 这些非正式规则(这一概念由诺斯提出)无时无刻约束着大家。这些制度实际上具有相当大的执行弹性,我们不能单纯从资源利用最大化的角度理解非正式规则。
也就是说,制度演化混杂了太多非理性因素与非物质因素,尤其是文化宗教这类。如何认识这种制度中非最优、非完全理性的制度演化,制度经济学又分为了基于积极运用新古典经济新制度经济学学派(如 Dron)和抛弃新古典经济学的旧制度经济学派(例如萨缪尔森(Samuelson))。(这只是诺斯的一种分法)
一些区分标准:制度的定义;理性与非理性假设边界;制度演化是否自发,相对经济外生还是内生;制度变迁的动力;人在制度变迁的地位;用经济解释制度还是用制度解释经济……
换句话讲,比起将集体作为一个单位,制度经济学注重“人——集体——制度——发展”的互动和动态演化。
新旧制度经济学的区别其实很模糊,制度经济学、发展经济学在历史上成为了一个什么都能装的大概念。
随便一提,杨小凯5也受到布坎南(Buchanan)社会选择理论的影响,其超边际分析也注重个人基本单位下的一般均衡传导路径。
此处可参考《发展经济学:边际分析与超边际分析 (导论)》
古典政治经济学把财政当成一个自发为集体谋福利的机构,但是从制度经济学来看,现实并非如此。财政其实可以被看作一种集体决策。集体政策就是一种制度设计。
财政学至今依旧在争议财政是什么,这一点难道不奇妙吗?
请思考思考,集体决策这个过程像不像一个学科——政治。
新制度经济学发展到后期,就变成了新政治经济学。
新政治经济学研究点之一——个体偏好到集体决策的偏差。
我被震惊的是这种从本质到手段的数学描述方式:
- 什么是公平?我们说不清楚,于是我们先研究推动公平的工具——财政。
- 什么是民主?我们说不清楚,于是我们先研究实践民主的工具——集体决策。
于是社会选择理论诞生了,例如委托代理6、官员晋升锦标赛7、包容性增长。今天我想介绍的就是社会选择理论中的投票相关的分析。一切集体决策都可以看作一种投票。
将研究范围定位到“做选择”这一思想也是经济学帝国主义的原因之一。
国际上还有许多大佬做拍卖设计的。这种微观理论的选题,几乎就是博弈论和数理分析了。
社会选择理论
本节参考自《高级微观经济学(第二版)》(蒋春殿)第 18 章。我基本上就是选择性复制粘贴而已。
关于更通俗的阿罗不可能解释,可以参以下视频:
社会福利泛函
我们曾在概率论中使用集合表示事件结果范围,而泛函之所以为“泛”,就是因为它研究的函数是集合空间到集合空间的映射,我们变为研究一类映射函数,也可以说,“泛”在研究对象是函数之函数;非线性泛函则是一种路径最优化,可以参考另外一篇博客《变分法学习笔记》。
高级微观的一些推理依赖集合作为决策要素的空间进行表达:
记社会个体集合为 $I=\{ 1,2,\ldots,n \}, n\geqslant2$。
$x,y \in X$ 作为资源集合,被分配到个体集合 $a_i$ 中,也就是 $\sum_i^n a_i=X_i$。
偏好有如下表。
- $x\succeq_{i}y$ :个体 $i$ 认为 $x$ 不次于 $y$ 。
- $x\sim_{i}y$ :个体 $i$ 认为 $x$ 和 $y$ 无差异。
- $x\succ_{i}y$ :个体 $i$ 认为 $x$ 优于 $y$ 。
之前提过了,泛函就是空间到空间的映射。而社会福利泛函就是个体联合偏好空间到社会偏好空间的映射,记为
$$ \succeq^{F}=F(\succeq_{1},\succeq_{2},\ldots,\succeq_{n}) $$
注意,这里是所有个体的偏好空间到社会偏好的映射,并不一定是数轴空间($R^1$)。个体联合偏好空间可以理解为所有人偏好的结果的集合,社会偏好空间可以理解为最后我们应该承认的总体偏好结果空间。
接下来举例说明:
对于独裁者社会来说,就是社会偏好被迫服从一个个体的偏好。
$$ x\succ_{h}y\quad\Rightarrow\quad x\succ y $$
多数票制就是少数服从多数的映射,按照同类个体偏好的加总进行比较。
$$ N(x\succ_{i}y)>N(y\succ_{i}x)\Rightarrow\quad x\succ y $$
$$ N(x\succ_{i}y)=N(y\succ_{i}x)\Rightarrow\quad x\sim y $$
梅伊定理(May): 社会福利泛函是多数票的充分必要性是以下三个性质:
- 多数票的匿名性是同一偏好内部的序列标识 $i$ 可以互换;
- 中立性表现为每个人票的权重是一样的;
- 正响应性表现为社会偏好改变方向和某些个体的偏好方向变化相同。
多数投票的想象很美好,但现实的投票会遇见各种问题,详细可查看“投票悖论”(又叫孔多塞悖论)。
由于偏好是基于序数效应论,是比较出来的。有可能出现下面这种无限循环的比较情况。现实投票更加复杂,例如美国大选摇摆州是关键,见风使舵、打击报复的心态也会影响投票结果。
因此,我们需要设置社会福利泛函的公理条件:
- 无限制性:每个个体偏好都能得到社会偏好(社会偏好至少满足传递性和完备性)
- 非独裁性:补充:匿名性原则的限制比非独裁性的约束还要强。
- 帕累托原则:$\forall i\in A, x\succ_{i}y \rightarrow x\succ y$
- 独立性:$\forall x, y\in X$ 当 $x\succ y$ 成立时,任何 $i\in I$ 在 $\{x, y\}$ 补集上的偏好不影响此时的社会偏好结果 $x\succ y$ 。独立性其实为了使得模型更加简洁,让投票者考虑的信息局限在当前选择之类,这一约束比中立性约束更弱。
此时我们可以提一种投票方案——博达计数方案。
核心就是排序,每个人按照从 1 到 n 的顺序对每一个选项排序 $c_i(x)$,越好越靠前,
最后将每个选项的顺序加总。 $$ c(x)=\sum_{i=1}^{n}c_{i}(x) $$ 总数越小,社会偏好越靠前。
$$ c(x)<c(y)\quad\Leftrightarrow\quad x\succ y $$
看起来很靠谱?但是博达计数方案违背了独立性:
为了讨论独立性,我们引入第三个选择 $z$
假设有两个个体,有如此偏好:
$$x\succ_1z\succ_1y,\quad y\succ_2x\succ_2z$$ 两两排序比较进行计数:
$$ c_{1}(x)=1, c_{2}(x)=2\quad\Rightarrow\quad c(x)=c_{1}(x)+c_{2}(x)=3$$
$$c_{1}(y)=3, c_{2}(y)=1\quad\Rightarrow\quad c(y)=c_{1}(y)+c_{2}(y)=4 $$
于是得到社会偏好 $x\succ y$。
但是假设我们改变 $z$ 在其中的顺序:
$$ x\succ_{1}y\succ_{1}z,\quad y\succ_{2}z\succ_{2}x $$ 得到如下计数:
$$ c_1(x)=1, c_2(x)=3\quad\Rightarrow\quad c(x)=c_1(x)+c_2(x)=4 $$ $$ c_1(y)=2, c_2(y)=1\quad\Rightarrow\quad c(y)=c_1(y)+c_2(y)=3 $$
社会偏好 $y\succ x$ 竟然发生了逆转!
从直觉上,个人感觉可以如下理解。博达计数方案不满足独立性的原因是它是基于排序记分,这种排序分数的一部分解释实际衡量的是 x、y 相对于 z 的偏好分数。
阿罗不可能定理
决定性集团
我们对于集体决策有很多期望,于是我们会思考,有没有投票方式能满足我们所有诉求?阿罗不可能定理证明的是——选项大于等于 3 时,这种期望不可能。
决定性偏好是指,特定情况下,部分群体拥有话语权会左右社会偏好。
集团 $K \in I$
$$ \forall i\in K, x\succ_iy;\quad\forall j\in I\cap K^c, y\succ_jx\quad\Rightarrow x\succ y $$ 也就是 $I$ 中分为 $K$ 和 $I\cap K^c$ 两种偏好立场,即便他们观点相反,但可能最后社会偏好反应的其实是 $K$ 的偏好。
- 美国大选摇摆州。
- 刚好平票的时刻,最后一票量将成为质变的岔路口。
- 明星表态和跟随明星的粉丝。
当集团 $K$ 的偏好直接决定了选项 $(x,y) \subset X$ 的社会偏好,则 $K$ 是社会福利泛函下的一个决定性集团,记作 $D_K(x,y)$。
再次补充:此处泛函是空间到空间的映射,由于 $K$ 决定了社会偏好,此时该集团的偏好就是个体联合偏好空间到社会偏好的映射。自然,当 $K$ 只有一个人时,就是独裁。
同时满足无限制性、帕累托原则、独立性时,决定性集团有以下性质:
- $(x,y) \subset X$ ,有决定性集团 $D_K(x,y)$,则当 $(u,v) \subset X$ ,也有 $D_K(u,v)$
- $K\subseteq I,J\subseteq I$ (符号含义是包含于或等于)都为决定性集团,则 $K\cap J$ 也是决定性集团。
- 任取 $K\subset I$,$K$ 和 $I\cap K^c$ 中必有一个决定性集团8。
- $K\subset I$ 是决定性的,$J\subset I$ 是任何包含了 $K$ 的集团,$J\subset K$ ,则 $J$ 也是决定性的。
- $K\subseteq I$ 是决定性的,且成员数量大于 1,存在真子集 $J\subset K$ 为决定性的。
关于这些性质的证明此处不再记录。
阿罗不可能定理
这是阿罗的博士论文……
定义:选择数量不低于 3(比如美国大选其实是两党制,用不上),不存在同时满足无限制性、非独裁性、帕累托原则、独立性的社会福利泛函。
关于其证明其实就是运用下面的性质:
- $(x,y) \subset X$ ,有决定性集团 $D_K(x,y)$,则当 $(u,v) \subset X$ ,也有 $D_K(u,v)$
- $K\subseteq I,J\subseteq I$ (符号含义是包含于或等于) 都为决定性集团,则 $K\cap J$ 也是决定性集团。
- 任取 $K\subset I$,$K$ 和 $I\cap K^c$ 中必有一个决定性集团8。
- $K\subset I$ 是决定性的,$J\subset I$ 是任何包含了 $K$ 的集团,$J\subset K$ ,则 $J$ 也是决定性的。
- $K\subseteq I$ 是决定性的,且成员数量大于 1,存在真子集 $J\subset K$ 为决定性的。
例如,证明满足无限制性、帕累托原则、独立性的社会福利泛函一定是独裁的:
社会整体 $I$ 可以被看作一个决定性集团,基于性质 5 可以无限套娃分解为一个。接下来有利用性质 2 对选择进行偏好分类,验证这个个体确实相对于其他选项属于独裁。
推荐参考:
- 当民主遇上逻辑——阿罗不可能定理 - 遥远地方剑星的文章 - 知乎
- 阿罗不可能定理(Arrow’s impossibility theorem) 」为什么反直觉?
- 已知阿罗的不可能定理的前提下,微观经济学为什么还要研究社会福利函数?
个人理解:
可以把阿罗不可能定理的这个独裁证明看作“量变到质变”的最后一票。 但理解需要更深一些:
记住:阿罗不可能定定理研究的是个体偏好空间到社会偏好空间的映射。
因为阿罗要解决的是个体偏好空间到社会偏好空间的最好映射,最理想的民主就是不存在那“质变一票”。
人人绝对平等,通过排序参与而不是基数效应加总。当然,早就有定理证明了序数与基数偏好的转化存在性。
假设人人都在未知的情况下一次性投票,总会有一个人的偏好决定了(即便他不知道自己属于这场游戏的独裁者)全社会的偏好,于是投票是独裁的。也就是说,此时映射并不是理想的,也不能真正反应大部分人的偏好。
假设多阶段博弈,人们可能基于打击报复的心态改变自己的投票,自己的偏好改来改去,此时违背了独立性假设,都为了胜利更改初心了,也就更没有真正反映出最好的映射了。
归根结底,阿罗不可能定理想要证明的是这种观点——个人偏好映射为社会偏好困难重重。
放宽假设
一种证明是参与者为正无穷时,阿罗不可能定理有解,但似乎并不像计量一样能搞渐进性。
放宽无限制假设,限制只有单峰偏好,没有多峰偏好。
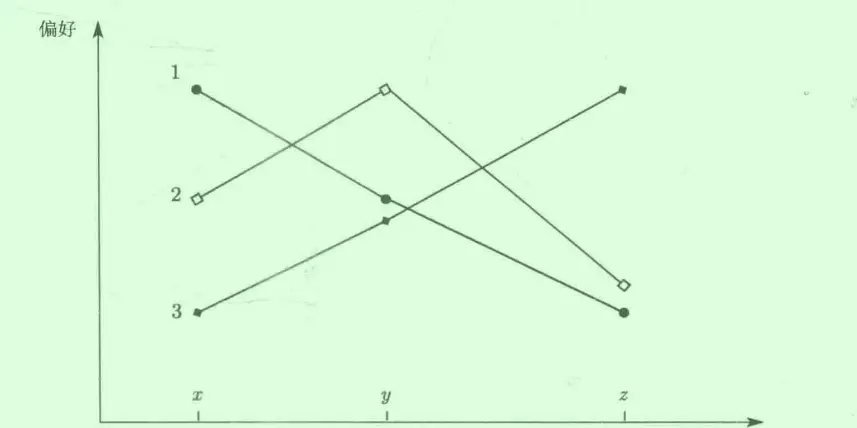
- 单峰偏好:如果选民偏离其最满意的结果,不论偏离的方向如何,其效用是下降的。
- 双峰偏好:如果选民偏离其最满意的结果,其效用先降后升。
其实就是把投票悖论(孔赛多悖论)的情况排除掉。 单峰偏好在连续封闭区间内需要是凸偏好。
陶哲轩的证明
阿罗不可能定理有很多种证明思路。
- 中级微观的一般介绍的表格排序。
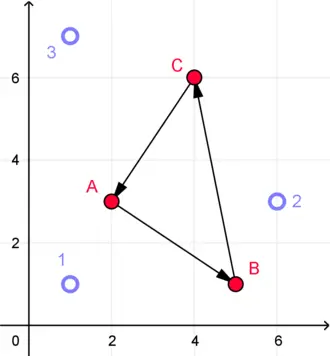
- 还有一种常见的是简化为二维坐标图研究偏好区块。
- 高级一般会选择泛函与集合论的证明,也就是本文的证明。
陶哲轩也曾给出过自己的证明:
解析可以参考:
高等概率论老师曾评价到——他为陶哲轩把部分精力放在非世界级难题上的做法感到惋惜😂。
-
这种讨论第一性的问题,我觉得都非常有意思。 ↩︎
-
广场、国防安全这类面向公众的,所有人都能享受(非排他性),且多一个人不影响质量的(非竞争性)的供给需要政府支持。 ↩︎
-
假设我们不知道我们要投胎到哪个社会,我们往往假设自己总投胎到最坏的社会,这种情况下社会福利的最好标准是最小值。 ↩︎
-
其他我知道的还有戏剧舞台论、自我映射论 ↩︎
-
社会选择理论提出者,诺奖得主布坎南(Buchanan)很欣赏杨小凯,因此杨小凯才被誉为最接近诺贝尔经济奖的国人。 ↩︎
-
交叉到博弈论、信息不对称。我们选举出的代表人和我们处于信息不对等的地位,我们不能使用权力契约描述这种情况,使用代理人更加客观。 ↩︎
-
官员是为了自己的晋升制定地方发展政策,因此注重基础设置这种有形的投入而非人力资本这种无形资本,同时大力举债,和对手相互较劲。提出者是北大的周黎安教授。 ↩︎